о чём на самом деле шутит xkcd / Хабр
Xkcd — один из самых культовых веб-комиксов, и минималистичный стиль зарисовок будто из учебника механики стал его визитной карточкой. Автор комикса Рэндел Манро признавался, что старательно ищет вдохновение для новых выпусков: он пробует новые программы и игры, работает над математическими задачами, следит за новостями науки и технологий. Если бы он этого не делал, то комикс рассказывал бы о том, как художник сидит дома за компьютером.Иногда выпуск комикса xkcd — это поверхностная шутка в узкой области знаний. Понять такой юмор сможет специалист или хотя бы слабо знакомый с затрагиваемой областью, а остальные будут лишь недоумевать. Пример такого выпуска — xkcd.com/977 Map Projections 2011 года. Для полного понимания выпуска нужно лишь примерно представлять историю и функцию различных проекций карт мира, иначе комикс останется чёрно-белым рисунком.
Даже внешне однозначные вопросы имеют несколько решений. Форма Земли — это похожий на шар геоид, но для удобства восприятия его лучше развернуть на плоскую карту.
Не все мы смотрим на карту для навигации в открытом море. Часто выбор метода преобразования формы Земли — это не вопрос жизни и смерти, это художественная иллюстрация. В этих случаях проекцию выбирают из устоявшихся вкусов и предпочтений — точно так же, как выбирают одежду или автомобиль. Можно смешно шутить про моду на дорогие кроссовки среди директоров крупных компаний Кремниевой долины или про популярность заниженных автомобилей. Точно так же шуткам поддаются предпочтения картографической проекции, как это и было сделано в Map Projections.
Разобьём комикс на несколько частей и рассмотрим их в удобном нам порядке.
Да, ты очень умный.
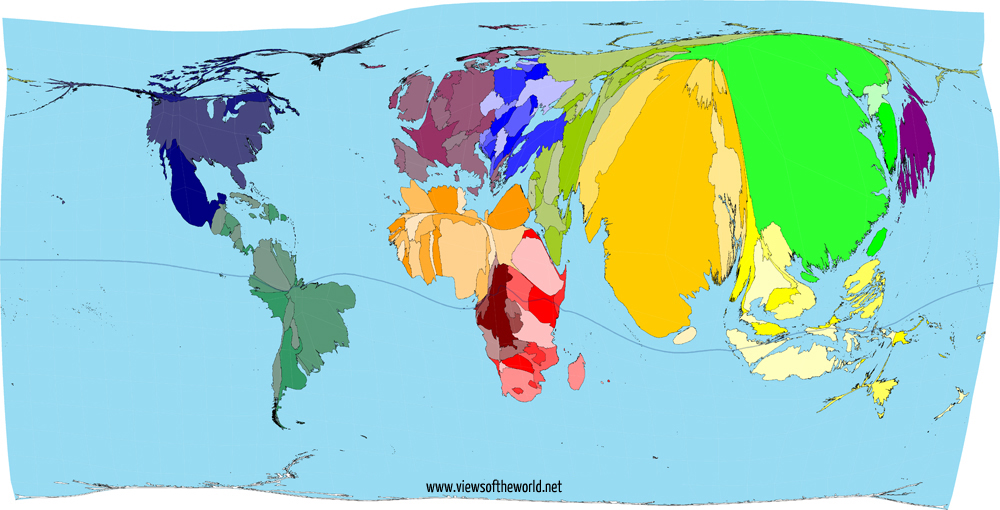
Земля — сложное тело с рельефом. Даже если принять её за шар, эллипсоид вращения или геоид, Землю всё равно не получится «сплющить» без искажений.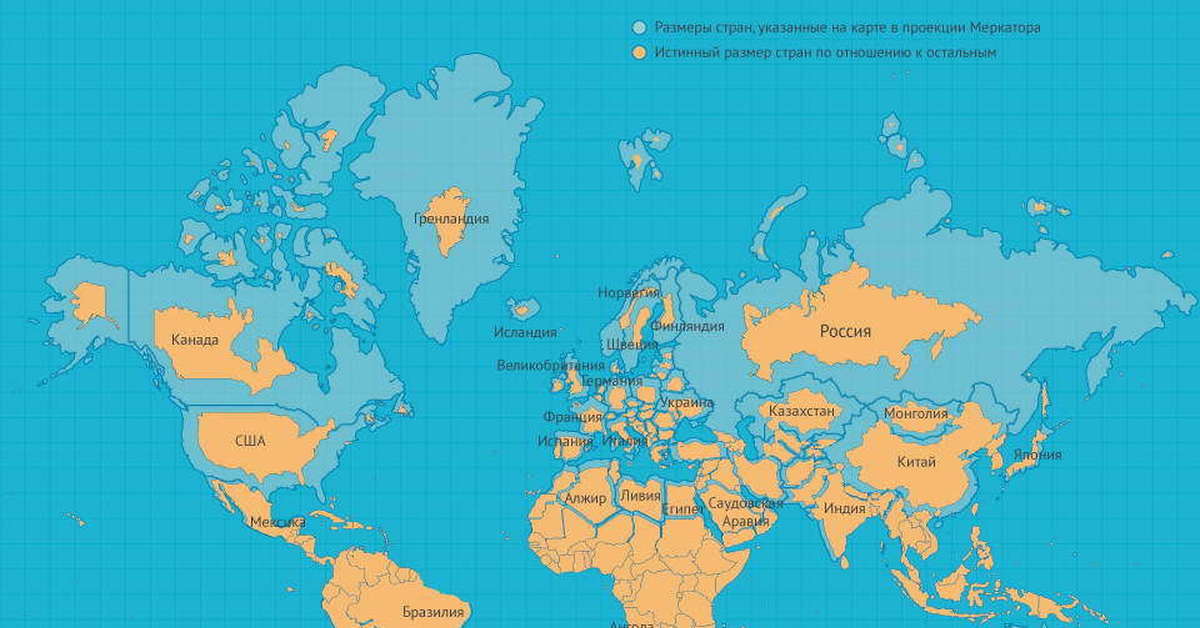
Искажаются длины рек и дорог, площади и формы стран и материков, углы для навигации. Любая проекция — это компромисс между тем, какие искажения нежелательны.
Поэтому любая попытка представить Землю на плоскости без искажений обречена на провал, о чём напоминает этот вариант ответа. Зачем пытаться сделать невозможное? Легче всего на вопрос о любимой картографической проекции самодовольно выкрикнуть: «Глобус!»
Понятно, что это не проекция, а лишь попытка умничать. Манро указывает на это в подписи.
Тебе кажется, что эта подойдёт. Тебе нравится, как X и Y преобразуются в широту и долготу. Другие проекции всё усложняют. Ты хочешь, чтобы я от тебя отстал и дал спокойно поужинать.
Это одна из самых старых проекций карты мира — вероятно, её изобрёл Птолемей ещё до нашей эры. Геоид преобразуется в цилиндр и разворачивается на лист бумаги. Сохраняются расстояния вдоль экватора и всех меридианов, но углы и площадь искажаются. Такую проекцию удобно использовать в компьютерных геоинформационных системах: линейные координаты на проекции легко преобразуются в широту и долготу.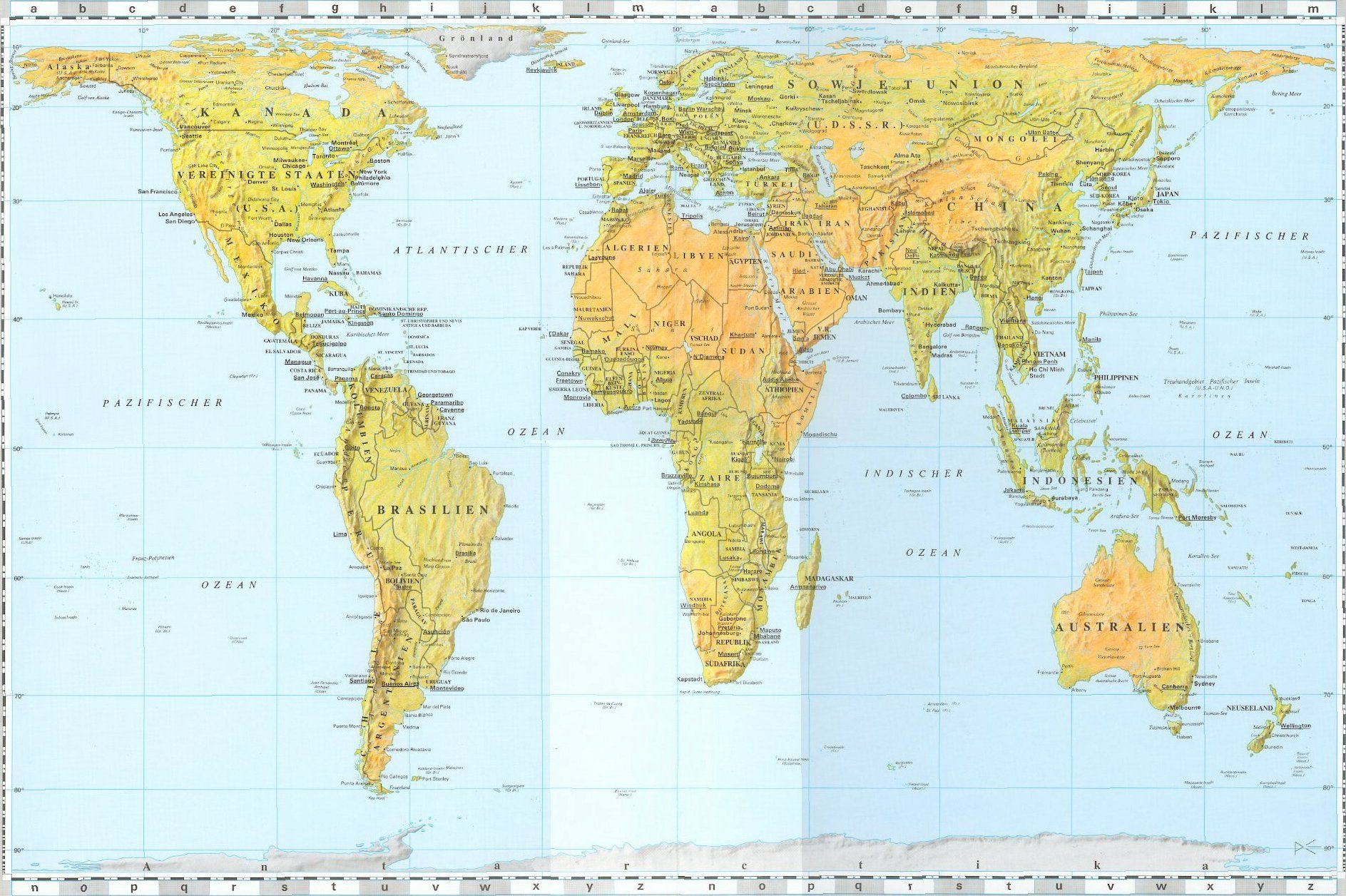
Равнопромежуточная проекция искажает углы и площади. Точки-полюсы на этой проекции растягиваются в линии. Из-за искажений равнопромежуточную проекцию не используют в навигации.
В представлении Манро такая проекция может понравиться занятому человеку, который не интересуется проекциями и связанными с ними премудростями.
Карты тебе малоинтересны.
В издании «Атласа» 1569 года фламандского картографа Герарда Меркатора на восемнадцати листах общим размером 202 на 124 сантиметра была представлена равноугольная цилиндрическая проекция. В названии заложены её характеристики: в каждой точке углы передаются без искажений, а параллели и меридианы сохраняют параллельность.
За это пришлось расплатиться искажениями масштаба: чем дальше объект уходит от экватора к полюсу, тем он крупнее. Сами полюса превращаются из точек в бесконечно большие объекты. Поэтому карта не простирается до полюсов, применяется отсечка по широтам в ±80°—85°.
Из-за этого не самая большая Антарктида приобретает в проекции Меркатора огромные размеры, а Африка и страны Южной и Юго-Восточной Азии кажутся меньше, чем на самом деле.
На проекции Меркатора Гренландия выглядит размером с весь Африканский континент, хотя на деле её площадь меньше площади Демократической Республики Конго.
Сайт The True Size Of демонстрирует, насколько сильно проекция Меркатора искажает площади.
Но проекция Меркатора пригодилась для навигации мореплавателей и, впоследствии, воздушного движения. Если стрелка компаса сохраняет своё положение, то траектория движения корабля в проекции Меркатора будет изображаться прямой линией. Пересечение двух дорог сохранит свой угол и в этой проекции. Проекция Меркатора широко используется в навигации и по сей день.
Более того, проекция Меркатора хорошо сохраняет общие очертания объектов. Вариант такой проекции используют все основные картографические сервисы: Google Maps, Bing Maps, OpenStreetMap и так далее. Отличие «веб-Меркатора» заключается в в том, что он отсекается на широтах в ±85,0511°, чтобы сделать карту идеально квадратной.
Задача картографической проекции решена, но не полностью.
Да, ходить по морю по Меркатору очень удобно, но не получится изобразить два небольших участка вокруг полюсов. Площади и длины искажаются. Подобная проекция может понравиться только тому, кому безразличны проблемы картографии, намекает подпись.
Я тебя ненавижу.
Обыватель привык к проекции Меркатора, которая нагло искажает реальные размеры стран вблизи экватора. Европа чуть ли не крупнее Южной Америки, хотя на деле она меньше почти в два раза. Гренландия на самом деле в 14 раз меньше Африки, хотя у Меркатора они выглядят примерно одинаково. Государства Европы и Северной Америки, выглядят крупнее, чем околоэкваториальные страны, что принижает важность последних. По крайней мере, примерно так звучит политически мотивированная критика проекции Меркатора.
В 1855 году шотландский священник Джеймс Галл описал проекцию, которая получила название «ортографическая проекция Галла». В этой проекции корректно отображаются площади объектов за счёт искажения их форм. На тот момент у проекции не было никаких политических подтекстов, это был побочный продукт астрономических наблюдений.
В 1967 году немец Арно Петерс создал идентичную проекцию, а в 1973 году, в период политического климата поиска социальной справедливости, представил её в виде нового изобретения. Проекция Петерса демонстрировалась как метод борьбы с империализмом и евроцентризмом. На проекции Меркатора Европа крупная и в центре, указывал автор, а на «новой» проекции Африка и близкие к экватору страны оказываются правильных размеров.
Само же название «проекция Галла — Петерса» впервые появилось в публикации Артура Робинсона 1986 года. Проекцию упоминают, к примеру, в телесериале «Западное крыло», который рассказывает о работе вымышленной администрации президента США. Сюжет подразумевает, что картографы предложили поменять карты в школах на «более социально справедливые».
Проблема проекции Галла — Петерса состоит в изначальном допущении о том, что проекция Меркатора ставит своей — основной или побочной — целью подъём значимости европейских государств за счёт их укрупнения на карте мира.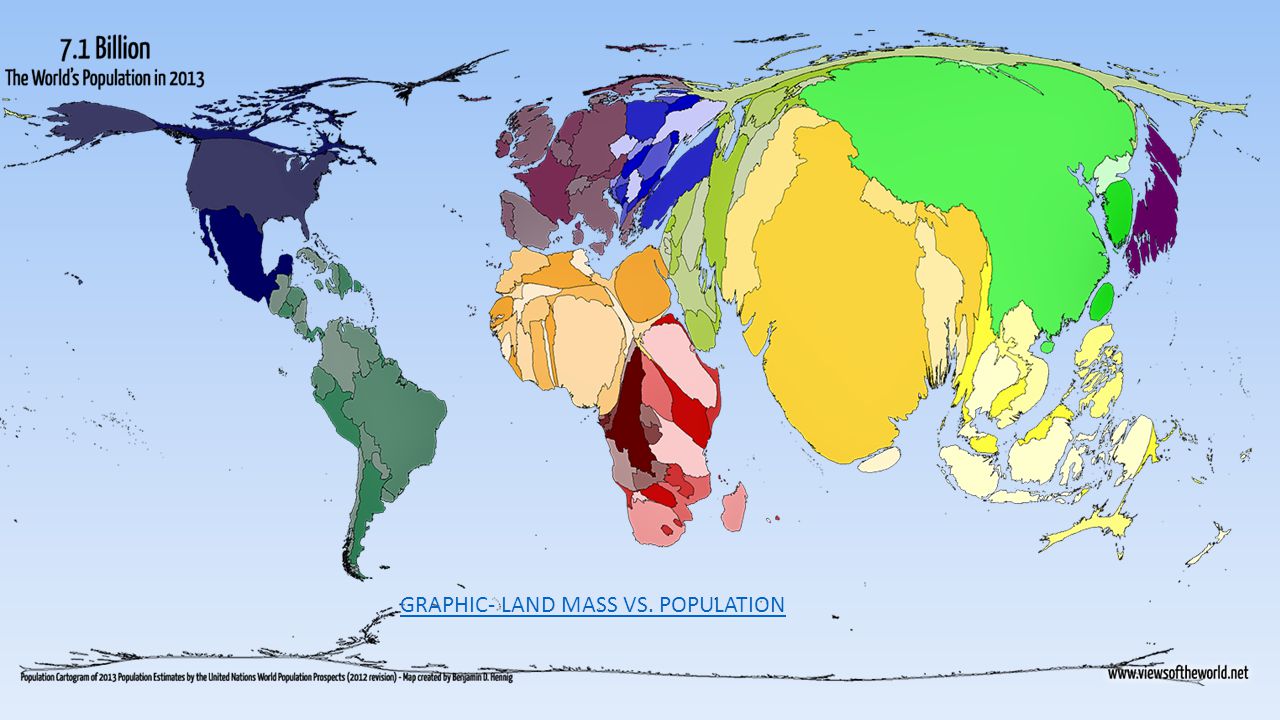
На самом деле проекция Меркатора лишь удобна для морской навигации, также она не искажает локальные формы объектов.Проекция Галла — Петерса сохраняет площади за счёт искажения углов, расстояний и формы объектов. Искажения значительны, хотя Петерс это отрицал. Несмотря на утверждения об обратном, проекция Петерса не представляет мир в том виде, в котором он выглядит на самом деле.
Самое забавное — это то, что эта карта наоборот изображает бедные страны у экватора с искажениями. Дело в том, что на этой проекции на 45 градусах северной и южной широты форма объектов не меняется относительно реальных. Чем дальше от этих двух линий, тем больше искажения формы. Одна из двух линий без искажений заходит на Европу — то есть тот район мира, от влияния которого проекция Галла — Петерса так стремится нас избавить. Таким образом, наиболее сильно у Петерса искажается Африка, хотя богатые «страны-империалисты» (Европа, США, Япония, Австралия) почти не меняют реальную форму.
Для сравнения: у проекции Бермана линия без искажений проходит на 30 градусах, у равновеликой цилиндрической проекции Ламберта — на экваторе.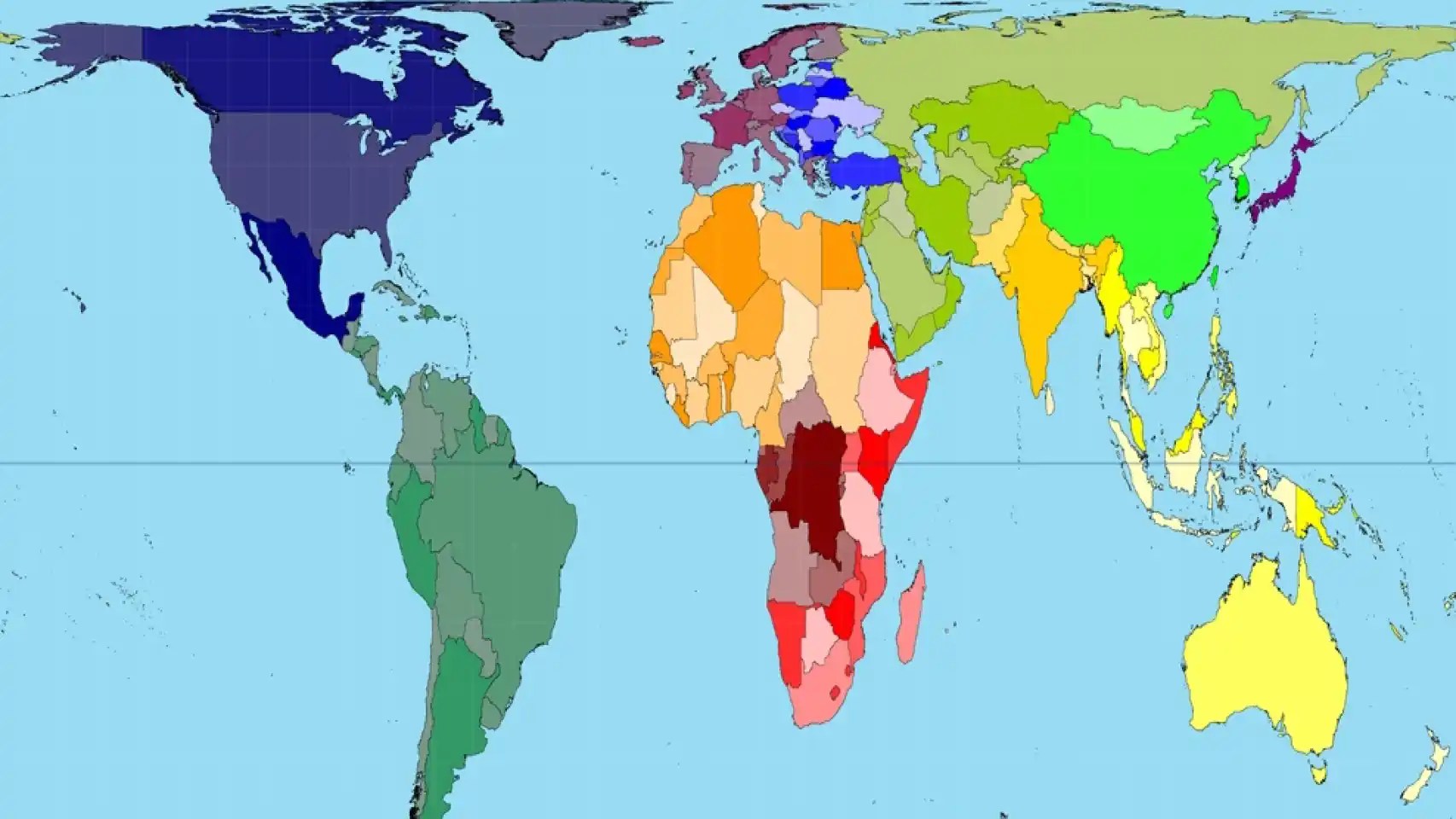
Эллипсы искажения на проекции Галла — Петерса
Карта в проекции Галла — Петерса прямоугольная, что немного странно для проекции в XX веке. До проекции Петерса уже существовали проекции с сохранением масштаба, хотя карту представили как нечто до этого невиданное. Наконец, если допустить, что чем больше страна, тем она воспринимается могущественней, то наиболее важной в проекции Меркатора будет Антарктида.
Если подытожить, то проекция Галла — Петерса находит проблему, которой не существует, не может её решить, но допускает множество новых искажений. Тем не менее, у неё находятся сторонники, которые искренне верят, что проекция Меркатора должна уйти в прошлое. К примеру, эту проекцию используют ЮНЕСКО, некоторые британские школы и часть школ штата Массачусетс.
Манро не ограничивается коротким замечанием, что ненавидит тех, у кого эта проекция любимая. Также в альт-тексте комикса он спрятал послание с шуткой в стиле Горацио Кейна: «Чего? Думаешь, мне не нравится карта Петерса, потому что вызов моим культурным допущениям вызывает у меня дискомфорт? А ты не думаешь, что сам не :: надевает очки:: проецируешь?»
Ты хочешь избежать культурного империализма, но про Галла — Петерса ты слышал плохое.
Ты неконфликтный и покупаешь органические продукты. Ты используешь недавно изобретённый набор гендерно-нейтральных местоимений и считаешь, что миру нужна революция в самосознании.В названии проекции Хобо — Дайера закодировано сразу три имени: Ховарда Бронстейна и Боба Абрамаса, менеджеров заказавшей проекцию компании ODT Maps, а также картографа Мика Дайера, который выполнил заказ. Она была создана в 2002 году как более приятный для глаза вариант Галла — Петерса.
Карта всё так же искажает формы стран. На 37,5° северной и южной широты искажений нет.
Эллипсы искажения на проекции Хобо — Дайера
Манро обыгрывает историю проекции, указав, что её любитель может оказаться менее радикальным и более неконфликтным сторонником социальной справедливости и заботы об окружающей среде. Такой человек покупает органические продукты, то есть выращенные с минимальным использованием синтетических удобрений, пестицидов и гербицидов. Он использует гендерно-нейтральные местоимения, чтобы никого не обидеть.
Перевёрнутая карта мира в проекции Хобо — Дайера
Ты считаешь, что когда мы смотрим на карту, на самом деле мы видим себя. После первого просмотра фильма „Начало“ ты шесть часов молча сидел в кинотеатре. Тебя пугает то, что внутри каждого из окружающих находится скелет. Однажды ты по-настоящему всмотрелся в свои руки.
Планета в проекции Пирса развёрнута так, что из проекции можно составить бесконечный узор. Она корректно передаёт углы во многих местах за исключением областей, где экватор и меридианы внезапно меняют направления. Экватор в проекции Пирса выглядит как квадрат, хотя у реального экватора острых углов нет. Сам Пирс утверждал, что искажённые области на карте занимают места меньше, чем у Меркатора.
Узор из Земли в проекции Пирса
У карт в проекции Пирса нет значимых практических применений. Зато сам алгоритм проекции пригодился для представления на плоскости 360-градусных изображений — Пирс удачно развернул сферу в прямоугольник, состоящий из двух квадратов.
Эллипсы искажения на проекции Пирса
Сюжет фильма «Начало» использует сложную вложенную структуру, поэтому зрителю может потребоваться несколько просмотров для полного осмысления кинокартины. При правильном настрое психики может казаться странным наличие в теле скелета или сложность кисти человеческой руки. Вероятно, Манро намекает, что бесконечный узор из проекций Земли и квадратность экватора нравятся людям, которые склонны фиксироваться на мелких деталях.
Ты человек несложный. Тебе нравится проекция Меркатора; тебе лишь хочется, чтобы она не была квадратной. Земля не квадратная, она круглая. Круги тебе нравятся. Сегодня будет отличный день!
В 1922 году Национальное картографическое общество США приняло в качестве стандартной карты мира проекцию Ван дер Гринтена. В этом статусе она просуществовала до 1988 года.
Эта проекция ни равновеликая, ни равноугольная. Она проектирует поверхность Земли в произвольную фигуру — круг. Она сохраняет знакомые по проекции Меркатора очертания материков и стран, незначительно убирая искажения.
При этом в полюсах искажение огромно — Антарктида будто крупнее всей остальной суши.
Эллипсы искажения проекции Ван дер Гринтена
Манро представляет поклонника такой проекции в виде откровенно глупого и наивного человека. Сфера и круг имеют мало общего, но для любителя Ван дер Гринтена это одно и то же. На самом деле этот человек недалеко отошёл от проекции Меркатора, намекает Манро.
У тебя есть удобная пара беговых кроссовок, которую ты носишь везде. Тебе нравится кофе и «Битлз». Ты считаешь, что проекция Робинсона — без вопросов лучшая.
Творение Робинсона сменило Ван дер Гринтена на посту проекции стандартной карты мира Национального картографического общества США в 1988 году. Десятилетие спустя, в 1998 году, проекцию сменили. Не исключено, что и сам автор комикса (Манро родился в 1984 году) учил географию с картой такой проекции.
Проекция Робинсона — это тоже ни равноугольная, ни равновеликая проекция, а компромисс. Меридианы нежно загибаются, а полюса вытягиваются в ниточки.
Поэтому на полюсах искажения огромны, но уже при небольшом отходе в сторону экватора ошибки не так значительны. Это во многом художественная картина мира: проекция задаётся таблицей значений с шагом в 5 градусов, а не формулой. Остальные значения получаются приближением.
Эллипсы искажения проекции Робинсона.
Манро намекает, что эта проекция привычна и приятна: он ассоциирует её поклонника с мягкими и комфортными вещами. Музыкальные вкусы людей фиксируются в подростковом возрасте. Возможно, Манро указывает, что такой человек вырос в эпоху популярности «Битлз», то есть это любящий спокойную жизнь человек за пятьдесят—шестьдесят.
Национальное картографическое общество приняло тройную проекцию Винкеля в 1998 году, но ты её обожал задолго до этого признания. Ты беспокоишься, что это конец, и подумываешь перейти на Каврайского. Однажды ты в отвращении покинул вечеринку, когда гость пришёл в обуви с пальцами. Название твоего любимого музыкального жанра начинается с „пост-“.
Тройная проекция Винкеля была опубликована в 1921 году, а в 1998 году Национальное картографическое общество приняло её в качестве стандартной. Это среднее арифметическое между равнопромежуточной проекцией и проекцией Айтофа — так картограф Освальд Винкель в своей компромиссной проекции попытался уменьшить все три типа искажений.
Популярный шуточный стереотип утверждает, что если некий продукт приобретает популярность, хипстеры немедленно отказываются от его употребления. Манро указывает, что поклонник тройной проекции Винкеля принадлежит к данной субкультуре. Такой человек откажется от неё в пользу неиспользуемой на Западе проекции советского геодезиста и картографа Каврайского, которая в целом похожа на тройную проекцию Винкеля.
Тебе нравится Айзек Азимов, XML и ботинки с пальцами. Ты считаешь, что у сегвеев просто плохая репутация. У тебя есть 3D-очки, в которых ты разглядываешь вращающиеся модели 3D-очков получше. Твоя раскладка — Дворак.
Зачем обязательно мучиться с шаром? Нашу планету можно приближённо представить в виде многогранника, а его развёртку сделать картографической проекцией.
Эту идею Бакминстер Фуллер опубликовал в журнале Life в 1943 году.
У этой развёртки есть несколько преимуществ. Искажения размеров и формы объектов меньше, чем на проекции Меркатора или Галла — Петерса. На такой карте удобно иллюстрировать научную теорию о миграции людей.
Эллипсы искажения проекции Димаксион
Вместе с тем нужно свыкнуться с несколькими новыми концепциями. На карте нет «верха» или «низа». Фуллер утверждал, что у Вселенной «север» и «юг» отсутствуют — есть только «внутри» и «снаружи». В проекции Димаксион трудно находить координаты объектов и указывать стороны света. Трудно находить пути для путешествий, они выглядят непредсказуемо.
Какими бы минимальными ни были искажения, но карты Земли нужны для передвижения по свету. Несмотря на оригинальность и красоту задумки, проекция Фуллера не получила какого-либо практического применения.
В подписи Манро собрал похожие случаи, когда внешне интересные изобретения на практике не имели значительного распространения, оставаясь чем-то нишевым.
В списке не самый популярный язык разметки XML, необычная обувь с пальцами, дорогие и оттого непопулярные мобильные скутеры фирмы Segway. Для 3D-очков (то есть ранних шлемов виртуальной реальности) Манро намекает на отсутствие контента и приложений — это справедливо для начала 2010-х годов. Раскладка Дворака призвана ускорить набор текста относительно машинописной QWERTY, но требует полного переучивания и не демонстрирует настолько значительных преимуществ на практике.
Серьёзно? Ты знаешь Уотермана? А что насчёт карты Кахилла 1909 года, на которой она основана… у тебя есть репродукция в рамке дома?! Ого… слушай, забудь про эти вопросы. Какие у тебя планы на вечер?!
Проекция Уотермана похожа на Димаксион: геоид примерно подобен многограннику, в данном случае — октаэдру. Затем многогранник разворачивают на плоскость. Как и в предыдущих случаях, форма объектов и их истинный размер искажаются не так сильно. Но на такой карте сложно указать стороны света и построить путь.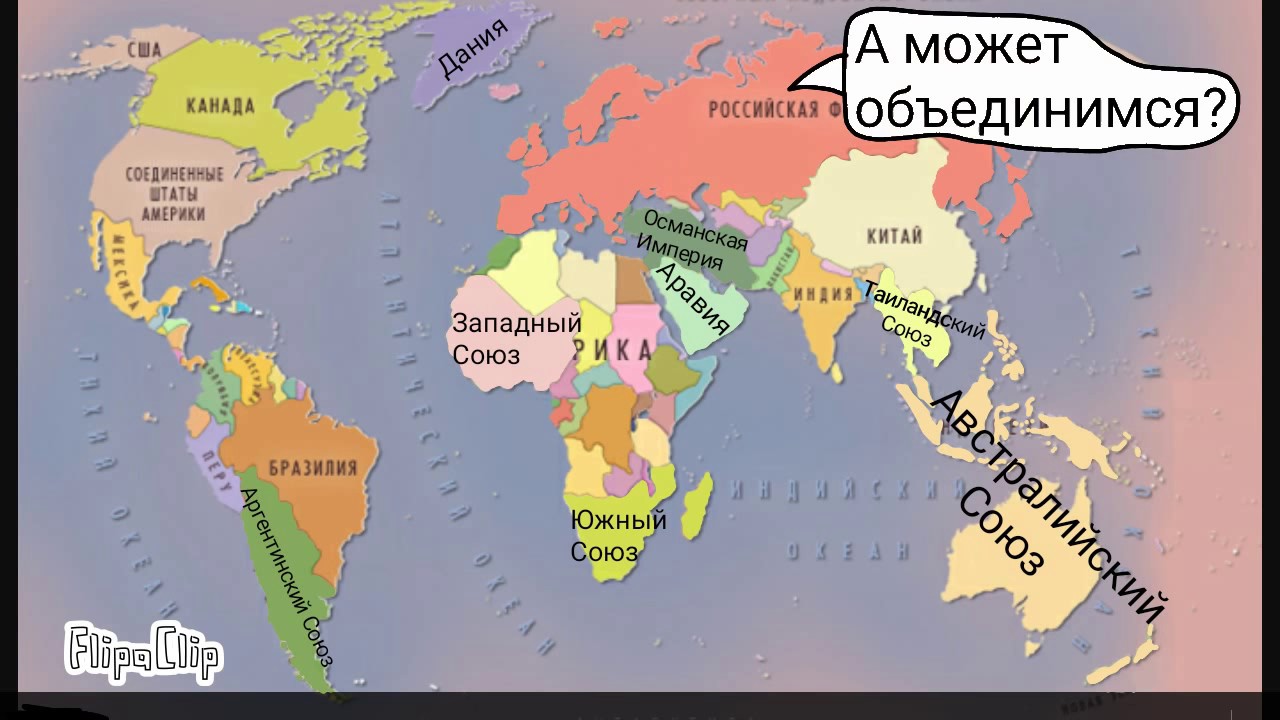
Уотерман опубликовал свою «бабочку» в 1996 году. Как напоминает Манро, она базировалась на работе Кахилла 1909 года. Архитектор Кахилл тоже покрошил Антарктиду на дольки, но делал это физически: он создал и запатентовал раскладной резиновый глобус, а потом сплющивал его.
Как и в случае с Димаксионом, эта проекция не получила значимого практического применения. Знать про неё может лишь большой поклонник картографии. Манро шутит, что ему есть о чём поболтать с человеком, который называет «бабочку Уотермана» своей любимой проекцией.
Говорят, перенос Земли на двумерную плоскость — это как расплющить кожуру апельсина, что для тебя звучит просто. Ты любишь простые решения. Ты считаешь, что проблем у нас было бы меньше, выбирай мы в Конгресс нормальных людей вместо политиков. Ты считаешь, что авиалиниям стоило бы просто закупать еду из ресторанов поблизости терминалов и подавать её на борту. Ты меняешь масло в своей машине, но втайне задумываешься, а нужно ли.
В 1923 году Джон Гуд разработал свою псевдоцилиндрическую равновеликую замену проекции Меркатора.
Проекция Гуда были призвана корректно передавать площади объектов. У проекции есть несколько разрывов по океанам и Антарктиде, которые выполнены для уменьшения искажений.
На некоторых вариантах проекции Гуда объекты повторяются. Можно выполнить такую проекцию с упором на океан.
Основной недостаток проекции Гуда — огромные промежутки в океанах, которые не позволяют визуально оценить расстояние между материками. Проекция Гуда призвана сохранять площади и выполняет это для материков. Но океаны в ней выглядят больше, чем на самом деле.
Действительно, за этой проекцией закрепилось сравнение с кожурой апельсина. Манро считает желание развернуть глобус в кожуру чрезмерно простым и неосведомлённым подходом к трудной проблеме, какой является картография. Он приводит в пример выборы в парламент: «нормальные» люди вряд ли бы смогли пробиться в строго выраженный правящий класс США. Да и в конечном итоге это вряд ли бы разрешило проблемы страны. К тому же, кто определяет «нормальность» человека?
Восприятие вкуса сильно зависит от состава воздуха и давления, а обычный ресторан не может единовременно заготовить нужные для 100—300 человек количества еды.
Также пища должна быть упакована специальным образом. Если заставить какой-то ресторан учесть все эти требования и поменять свои технологии, то он превратится в поставщика еды для пассажиров самолётов.
Производитель автомобиля указывает, когда менять масло. Наш любитель проекции Гуда иногда размышляет, а нет ли между автопроизводителями и продавцами автомобильного масла сговора.
Всё это — ловушки, в которые можно попасть, если недооценить решаемую проблему. Манро указывает, что и разворот геоида на плоскость не так прост, как кажется поклоннику проекции Гуда.
По материалам Brilliant Maps, обсуждения на «Реддите» и Explain xkcd.
Проекции в картографии
: 8 ноя 2012 , Недаром помнит вся Россия , том 46, №4С давних пор путешественники и мореплаватели занимались составлением карт, изображая в виде рисунков и схем изученные территории.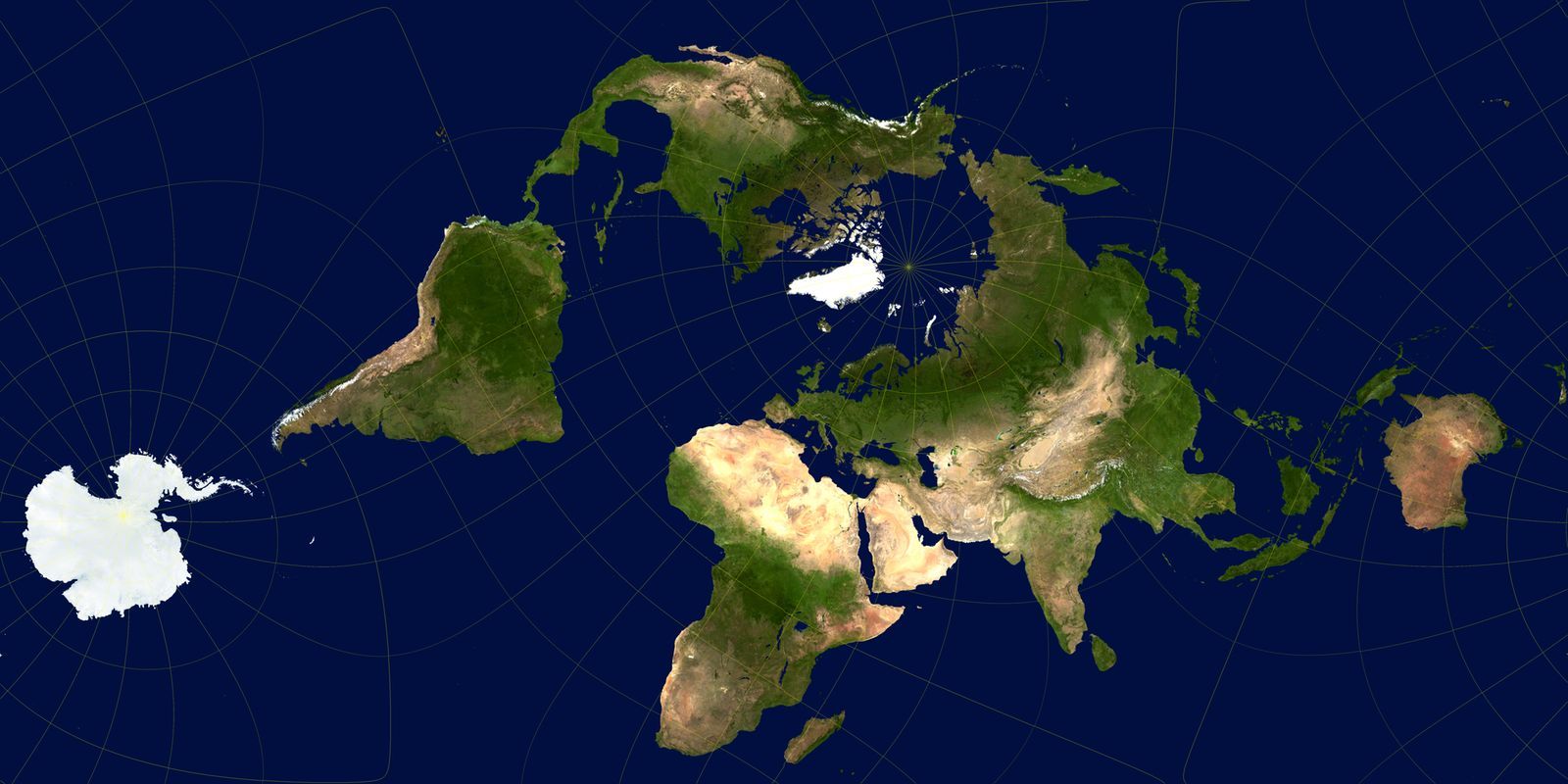
Исторические исследования показывают, что картография появилась в первобытном обществе еще до появления письменности. В современную эпоху благодаря развитию средств передачи и обработки данных, таких как компьютеры, интернет, спутниковая и мобильная связь, важнейшей составляющей информационных ресурсов остается геоинформация, т.е. данные о положении и координатах различных объектов в окружающем нас географическом пространстве.
Современные карты составляются в электронном виде с использованием аппаратов дистанционного зондирования Земли, спутниковой глобальной системы позиционирования (GPS либо ГЛОНАСС) и т. д. Однако сущность картографии остается прежней — это изображение объектов на карте, позволяющее однозначно идентифицировать их, определив положение при помощи привязки к той или иной системе географических координат. Неудивительно поэтому, что одной из основных и самых распространенных сегодня картографических проекций является равноугольная цилиндрическая проекция Меркатора, впервые примененная для создания карт четыре с половиной века назад
Работа древних землемеров не выходила за пределы геодезических измерений и расчетов для расстановки вех вдоль маршрута будущей дороги или обозначения границ земельных участков.
Но постепенно накапливалось множество данных – расстояния между городами, препятствия на пути, расположение водных объектов, лесных массивов, особенности ландшафта, границы государств и материков. Карты захватывали все большие территории, становились более детальными, но при этом возрастала и их погрешность.
Поскольку Земля представляет собой геоид (фигуру, близкую к эллипсоиду), для изображения поверхности геоида Земли на карте необходимо развернуть, спроецировать эту поверхность на плоскость тем или иным способом. Методы отображения геоида на плоской карте называются картографическими проекциями. Существует несколько видов проекций, и каждая из них вносит в плоское изображение свои искажения длин, углов, площадей или формы фигур.
Как сделать точную карту?
Полностью избежать искажений при построении карты невозможно. Однако можно избавиться от какого-либо одного типа искажений. Так называемые равновеликие проекции сохраняют площади, но при этом искажают углы и формы.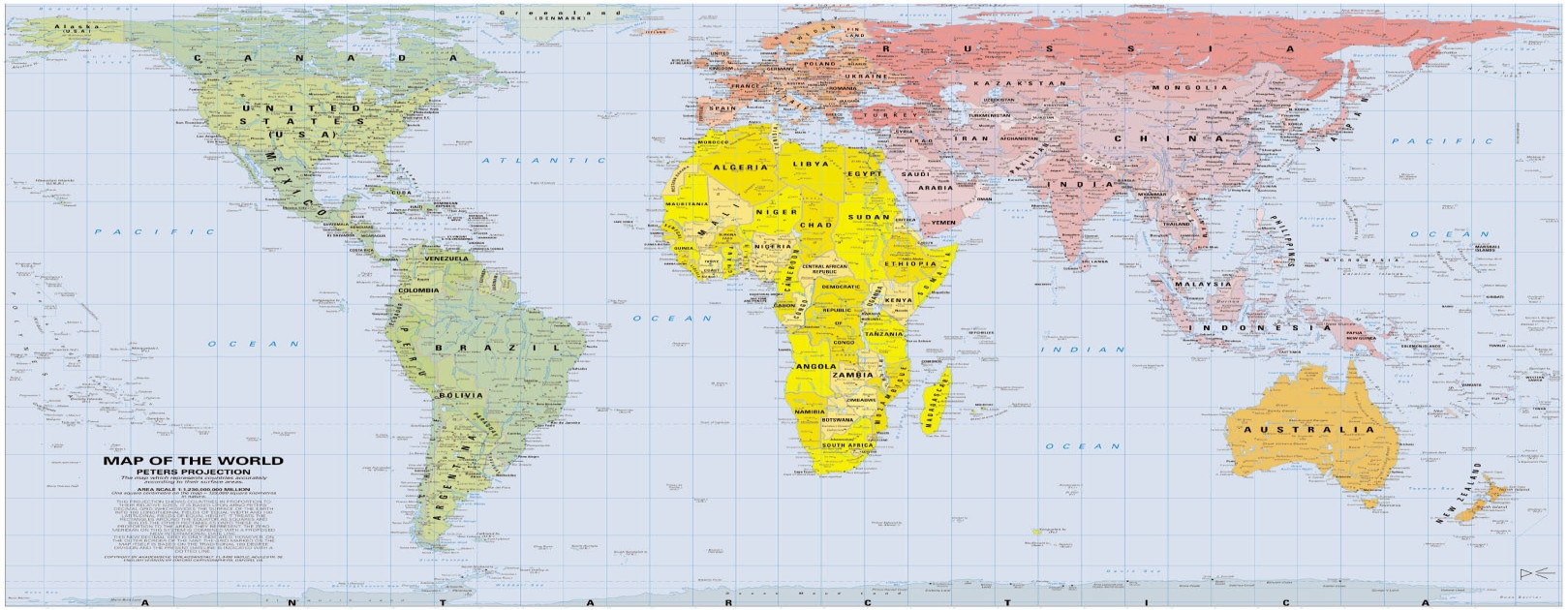
Равновеликими проекциями удобно пользоваться в экономических, почвенных и других мелкомасштабных тематических картах – для того, чтобы с их помощью рассчитывать, например, площади территорий, подвергшихся загрязнению, или управлять лесными хозяйствами. Примером такой проекции служит равновеликая коническая проекция Альберса, разработанная в 1805 г. немецким картографом Хейнрихом Альберсом.
Равноугольные проекции — это проекции без искажений углов. Такие проекции удобны для решения навигационных задач. Угол на местности всегда равен углу на такой карте, а прямая линия на местности изображается прямой линией на карте. Это позволяет мореплавателям и путешественникам прокладывать маршрут и точно следовать ему с помощью показаний компаса. Однако линейный масштаб карты при такой проекции зависит от положения точки на ней.
Самой древней равноугольной проекцией считается стереографическая проекция, которая была придумана Аполлонием Пергским около 200 г.
до нашей эры. Эта проекция и по сей день используется для карт звездного неба, в фотографии – для отображения сферических панорам, в кристаллографии – для изображения точечных групп симметрии кристаллов. Но использование этой проекции в мореплавании было бы затруднительным в силу слишком больших линейных искажений.
Проекция Меркатора
В 1569 г. фламандский географ Герхард Меркатор (латинизированное имя Герарда Кремера) разработал и впервые применил в своем атласе (полное название «Атлас, или Космографические рассуждения о сотворении мира и вид сотворенного») равноугольную цилиндрическую проекцию, названную впоследствии его именем и ставшую одной из основных и самых распространенных картографических проекций.
Для построения цилиндрической проекции Меркатора земной геоид помещают внутри цилиндра так, чтобы геоид касался цилиндра по экватору. Проекцию получают, проводя лучи из центра геоида до пересечения с поверхностью цилиндра.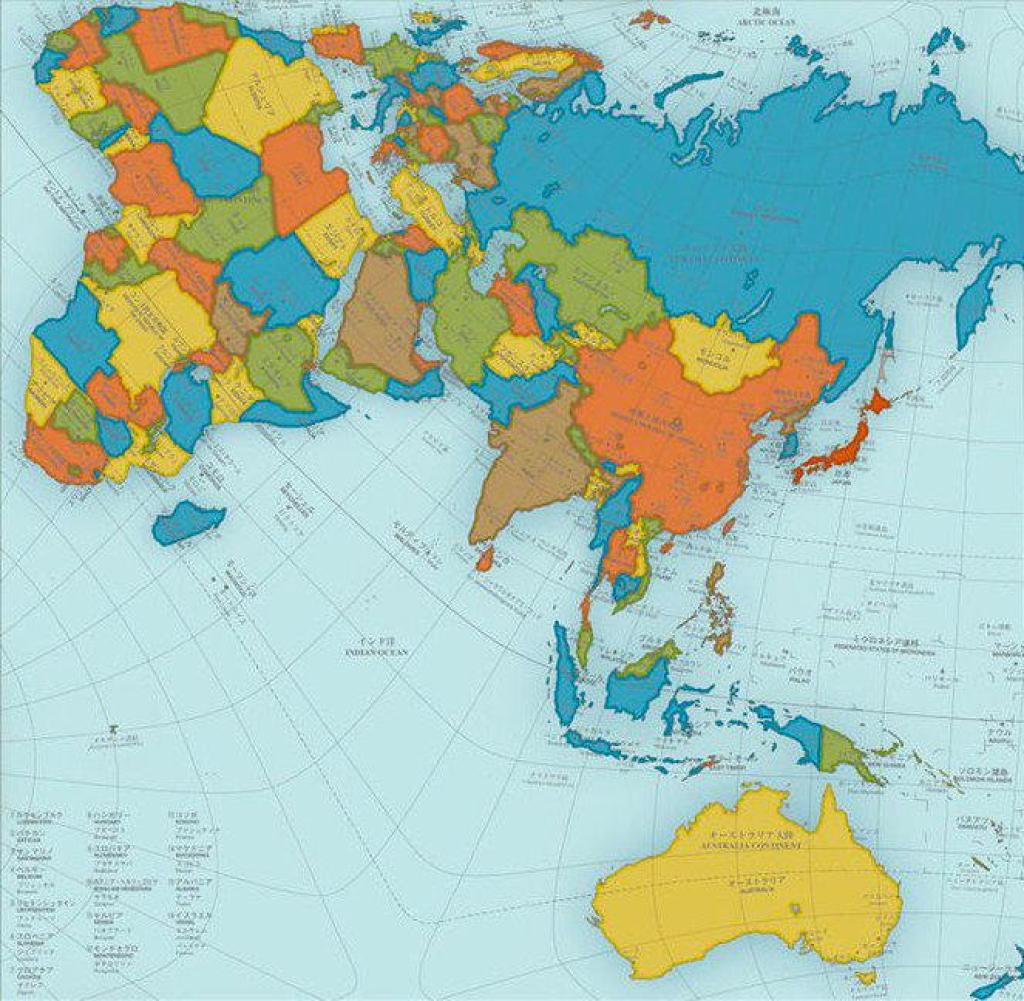
Если после этого цилиндр разрезать вдоль оси и развернуть, то получится плоская карта поверхности Земли. Образно это можно представить следующим образом: глобус оборачивается листом бумаги по экватору, в центр глобуса помещается лампа и на листе бумаги отображаются спроецированные лампой изображения материков, островов, рек и т. п. Если бы на бумагу был нанесен способный засвечиваться слой, то, развернув лист, мы получили бы готовую карту.
Полюса в такой проекции расположены на бесконечном расстоянии от экватора, и, следовательно, не могут быть изображены на карте. На практике карта имеет верхний и нижний пределы широт – примерно до 80° СШ и ЮШ.
Параллели и меридианы картографической сетки изображаются на карте параллельными прямыми линиями, при этом они всегда перпендикулярны. Расстояния между меридианами одинаковы, а вот расстояние между параллелями равно расстоянию между меридианами вблизи экватора, но быстро увеличивается при приближении к полюсам.
Масштаб в этой проекции не является постоянным, он увеличивается от экватора к полюсам как обратный косинус широты, но масштабы по вертикали и по горизонтали всегда равны.
Равенство вертикального и горизонтального масштабов обеспечивает равноугольность проекции – угол между двумя линиями на местности равен углу между изображением этих линий на карте. Благодаря этому хорошо отображается форма небольших объектов. Но искажения площади увеличиваются по направлению к полярным регионам. Например, несмотря на то, что Гренландия составляет всего одну восьмую размера Южной Америки, в проекции Меркатора она представляется больше. Большие искажения площадей делают проекцию Меркатора непригодной для общегеографических карт мира.
Линия, проведенная между двумя точками на карте в этой проекции, пересекает меридианы под одним и тем же углом. Эта линия называется румбом или локсодромией. Надо отметить, что эта линия не описывает кратчайшее расстояние между точками, но в проекции Меркатора всегда изображается прямой линией.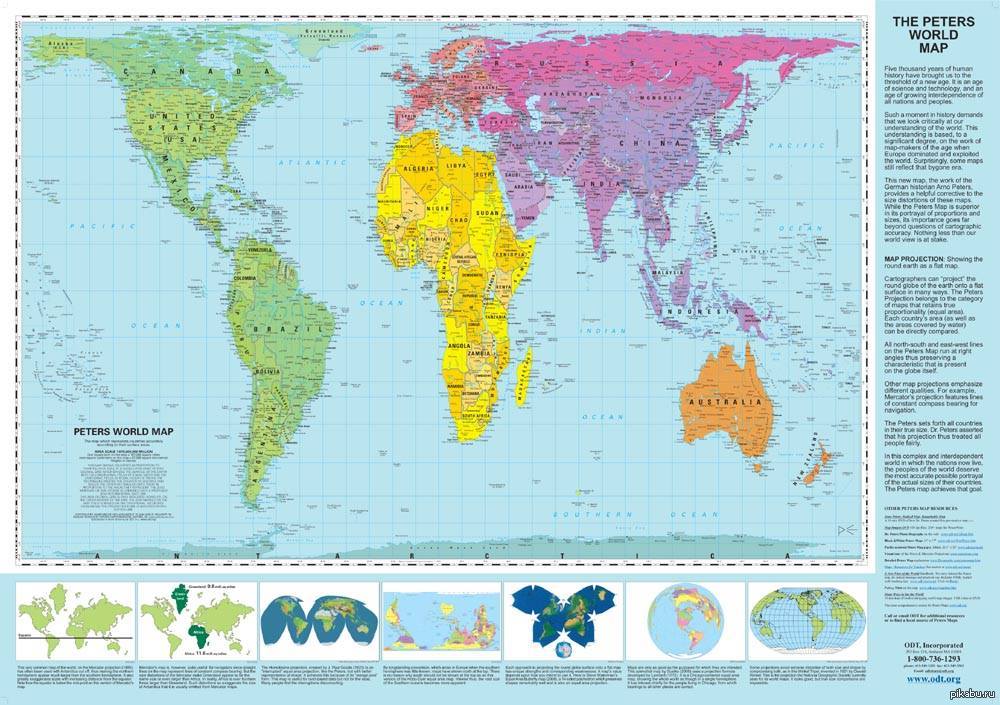
Этот факт делает проекцию идеальной для нужд навигации. Если мореплаватель желает отправиться, например, из Испании в Вест-Индию, все, что ему нужно сделать, это провести линию между двумя точками, и штурман будет знать, какого направления по компасу постоянно придерживаться, чтобы приплыть к месту назначения.
С точностью до сантиметра
Для применения проекции Меркатора (как, впрочем, и любой другой) необходимо определить систему координат на земной поверхности и корректно выбрать так называемый референц-эллипсоид – эллипсоид вращения, приближенно описывающий форму поверхности Земли (геоида). Для местных карт в России в качестве такого референц-эллипсоида с 1946 г. используется эллипсоид Красовского. В большинстве европейских стран вместо него используется эллипсоид Бесселя. Самым популярным в наши дни эллипсоидом, предназначенным для составления общемировых карт, является мировая геодезическая система 1984 г. WGS-84. Она определяет трехмерную систему координат для позиционирования на земной поверхности относительно центра масс Земли, погрешность составляет менее 2 см.
Классическая равноугольная цилиндрическая проекция Меркатора применяется к соответствующему эллипсоиду. Так, например, сервис Яндекс.Карты использует эллиптическую WGS-84 проекцию Меркатора.
В последнее время в связи со стремительным развитием картографических веб-сервисов большое распространение получил другой вариант проекции Меркатора – на базе сферы, а не эллипсоида. Этот выбор обусловлен более простыми расчетами, которые могут быть быстро выполнены клиентами этих сервисов прямо в браузере. Часто эту проекцию называют «сферическим Меркатором». Такой вариант проекции Меркатора используется сервисами Google Maps, а также 2ГИС.
Еще одним известным вариантом проекции Меркатора является равноугольная проекция Гаусса-Крюгера. Она была введена выдающимся немецким ученым Карлом Фридрихом Гауссом в 1820—1830 гг. для картографирования Германии – так называемой ганноверской триангуляции. В 1912 и 1919 гг. ее развил немецкий геодезист Л.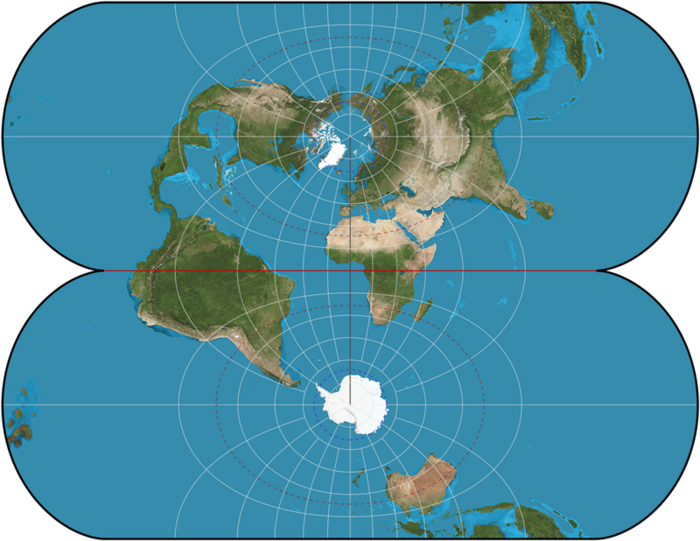
Крюгер.
По сути, она является поперечной цилиндрической проекцией. Поверхность земного эллипсоида делится на трех- или шестиградусные зоны, ограниченные меридианами от полюса до полюса. Цилиндр касается среднего меридиана зоны, и она проецируется на этот цилиндр. Всего можно выделить 60 шестиградусных или 120 трехградусных зон.
В России для топографических карт масштаба 1 : 1000000 применяют шестиградусные зоны. Для топографических планов масштаба 1 : 5000 и 1:2000 применяются трехградусные зоны, осевые меридианы которых совпадают с осевыми и граничными меридианами шестиградусных зон. При съемках городов и территорий под строительство крупных инженерных сооружений могут быть использованы частные зоны с осевым меридианом посередине объекта.
Многомерная карта
Современные информационные технологии позволяют не просто нанести контуры объекта на карту, но и менять его вид в зависимости от масштаба, связать с его географическим положением множество других атрибутов, таких как адрес, информация о расположенных в данном здании организациях, количество этажей и т.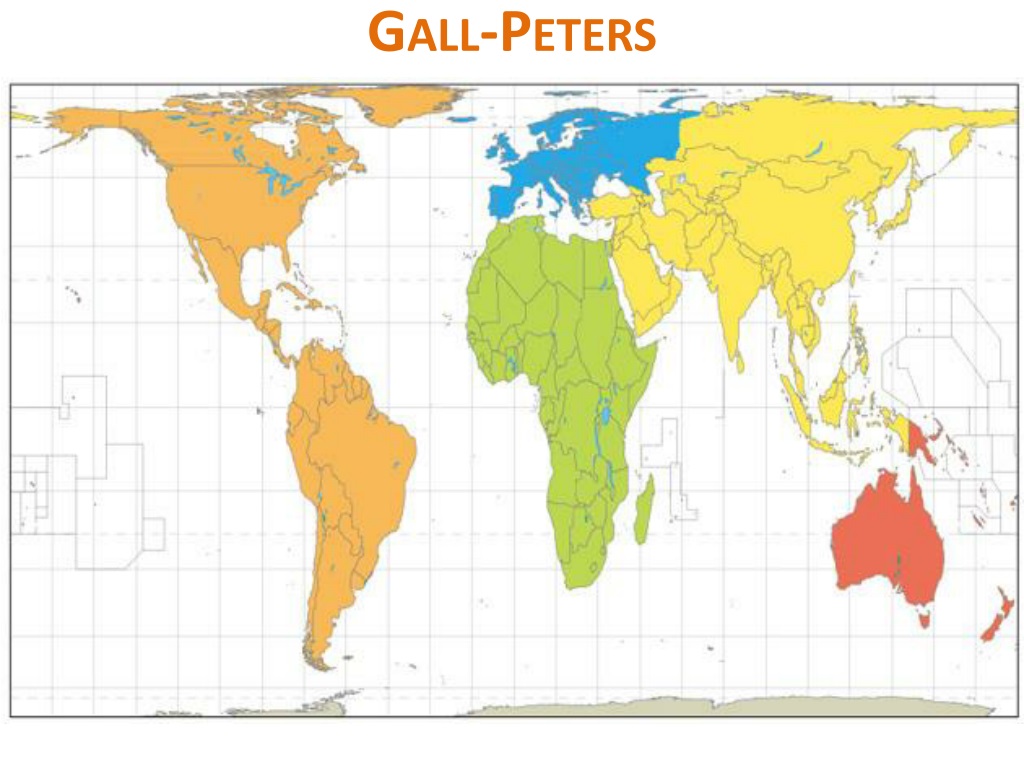
п., делая электронную карту многомерной, разномасштабной, интегрируя в ней одновременно несколько справочных баз данных. Для обработки этого массива информации и представления его в удобном для пользователя виде необходимы достаточно сложные программные продукты, так называемые геоинформационные системы, разработку и поддержку которых могут осуществить лишь достаточно крупные, обладающие необходимым опытом IT-компании. Но, несмотря на то, что современные электронные карты мало похожи на своих бумажных предшественников, все равно в их основе лежат картография и тот или иной способ отображения земной поверхности на плоскость.
Для иллюстрации методов современной картографии можно рассмотреть опыт работы компании «Дата Ист» (Новосибирск), занимающейся разработкой программного обеспечения в области геоинформационных технологий.
Проекция, которая выбирается для построения электронной карты, зависит от назначения карты. Для карт общего пользования и для навигационных карт, как правило, применяется проекция Меркатора с системой координат WGS-84.
Например, эта система координат использовалась в проекте «Мобильный Новосибирск», созданном по заказу мэрии города Новосибирска для городского муниципального портала.
Для крупномасштабных карт с целью минимизации линейных искажений используются как зональные равноугольные проекции (Гаусса-Крюгера), так и неравноугольные проекции (например, коническая равнопромежуточная проекция – Equidistant conic).
Сегодня карты создаются с широким привлечением аэрофотосъемки и спутниковых фотографий. Для качественной работы над картами в компании «Дата Ист» создан архив космических снимков, охватывающих территории Новосибирской, Кемеровской, Томской, Омской областей, Алтайского края, Республик Алтай и Хакасия, других регионов России. С помощью этого архива, кроме крупномасштабных карт территории, можно изготавливать схемы отдельных объектов и участков под заказ. При этом в зависимости от территории и необходимого масштаба применяется та или иная проекция.
Со времен Меркатора картография изменилась радикально. Информационная революция затронула эту область человеческой деятельности, наверное, больше всех. Вместо томов бумажных карт теперь каждому путешественнику, туристу, водителю доступны компактные электронные навигаторы, содержащие в себе массу полезной информации о географических объектах.
Но суть карт осталась той же – показать нам в удобном и ясном виде, с указанием точных географических координат, расположение объектов окружающего нас мира.
Литература
ГОСТ Р 50828-95. Геоинформационное картографирование. Пространственные данные, цифровые и электронные карты. Общие требования. М., 1995.
Капралов Е. Г. и др. Основы геоинформатики: в 2 кн. / Учеб. пособие для студ. вузов / Под ред. Тикунова В. С. М.: Академия, 2004. 352, 480 c.
Жалковский Е. А. и др.
Цифровая картография и геоинформатика / Краткий терминологический словарь. М.: Картгеоцентр-Геодезиздат, 1999. 46 с.
Баранов Ю. Б. и др. Геоинформатика. Толковый словарь основных терминов. М.: ГИС-Ассоциация, 1999.
ДеМерс Н. Н. Географические информационные системы. Основы.: Пер. с англ. М.: Дата+, 1999.
Карты любезно предоставлены ООО «Дата Ист» (г. Новосибирск)
: 8 ноя 2012 , Недаром помнит вся Россия , том 46, №4Какая картографическая проекция лучшая?
«Проблема апельсиновой корки», пожалуй, наиболее часто цитируемая аналогия, которую географы используют для объяснения того, почему трехмерный мир не может быть представлен в двух измерениях без каких-либо искажений. Как бы вы ни старались, вы просто не можете сгладить апельсиновую корку, не порвав, не раздавив или не растянув ее.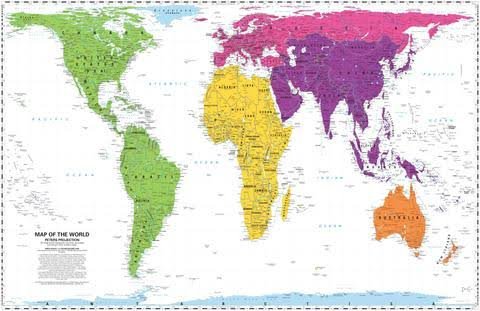
Точно так же, когда картографы пытаются сгладить Землю для картографической проекции, неизбежно возникают искажения с точки зрения формы, расстояния, направления или площади суши9.0003
В зависимости от цели, которой они пытаются служить, количество возможных картографических проекций безгранично. Однако какую картографическую проекцию следует использовать для общих целей, например, для вывешивания в классах или в телевизионных новостях? Вот как некоторые популярные прогнозы соотносятся друг с другом:
Меркатор
Самая популярная картографическая проекция в мире существует уже 448 лет. Он был создан фламандским картографом Герардусом Меркатором в 1569 году, когда Антарктида еще даже не была открыта. Меркатор был разработан как навигационный инструмент для моряков, поскольку на этой карте удобнее всего вручную прокладывать курсы с помощью параллельных правил и треугольников.
На большинстве карт, когда вы пытаетесь исправить один тип искажения, вы увеличиваете другой вид искажения.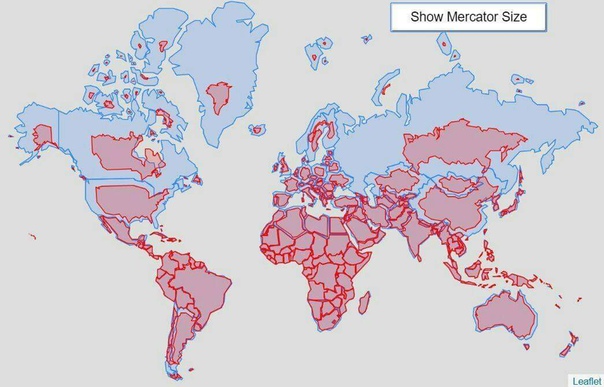
Тем не менее, Меркатор — одна из тех редких карт, чей ответ на широтное искажение заключался в том, чтобы гарантировать, что продольное искажение столь же плохо!
В проекции Меркатора Гренландия примерно такого же размера, как Африка. В реальности Африка почти в 14 раз больше, а Гренландия может поместиться внутри Китая не менее чем в четыре раза. Карта также предполагает, что скандинавские страны больше, чем Индия, тогда как Индия на самом деле в три раза больше. И все же Google Maps, Bing, Yahoo и даже OpenStreetMaps продолжают использовать ту или иную версию Mercator для отображения мира.
Плюсы: Морякам понравилось; сохраняет углы и направления на небольшой площади
Минусы: Плохо для понимания реальных размеров и формы континентов и стран
Связанный: После этого видео вы больше никогда не будете доверять карте
Галл-Питерс
Самая большая критика перекошенной проекции Меркатора поступила в 1973 году от немецкого режиссера и журналиста Арно Петерса.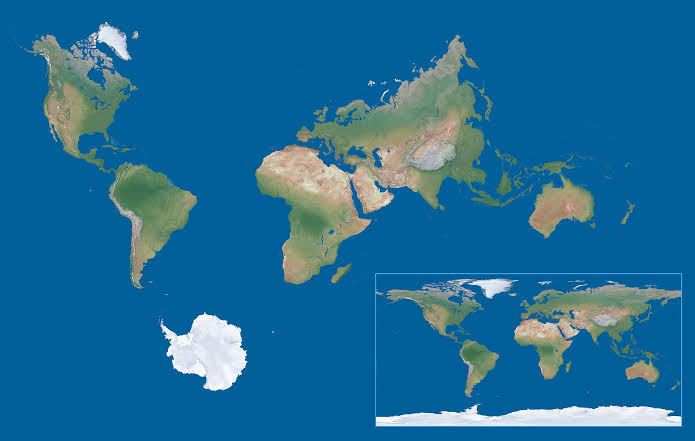
Петерс утверждал, что, увеличивая Европу и Северную Америку, карты Меркатора давали белым нациям ощущение превосходства над небелыми нациями.
Его решение? Равновеликая проекция, показывающая правильные размеры стран по отношению друг к другу. Не то чтобы в прогнозе Галла-Петерса не было недостатков. В своем стремлении устранить искажения размера карта растянулась в некоторых местах вблизи полюсов по горизонтали до шокирующей степени. Он также растянул суши по вертикали вблизи экватора. Итак, если карта кажется вам действительно странной, это потому, что все формы и углы неправильные — именно по этой причине мы редко видим эту карту в Интернете. Тем не менее, он довольно широко используется в британской школьной системе.
Достоинства: Единственная карта своего времени с «корректной местностью»; появился в Западном крыле (S2E16)
Минусы: Разозлило картографическое сообщество в 1980-х
Предложено: Знаете ли вы, как создавались карты Игры престолов?
Робинзон
Американский географ и картограф Артур Х.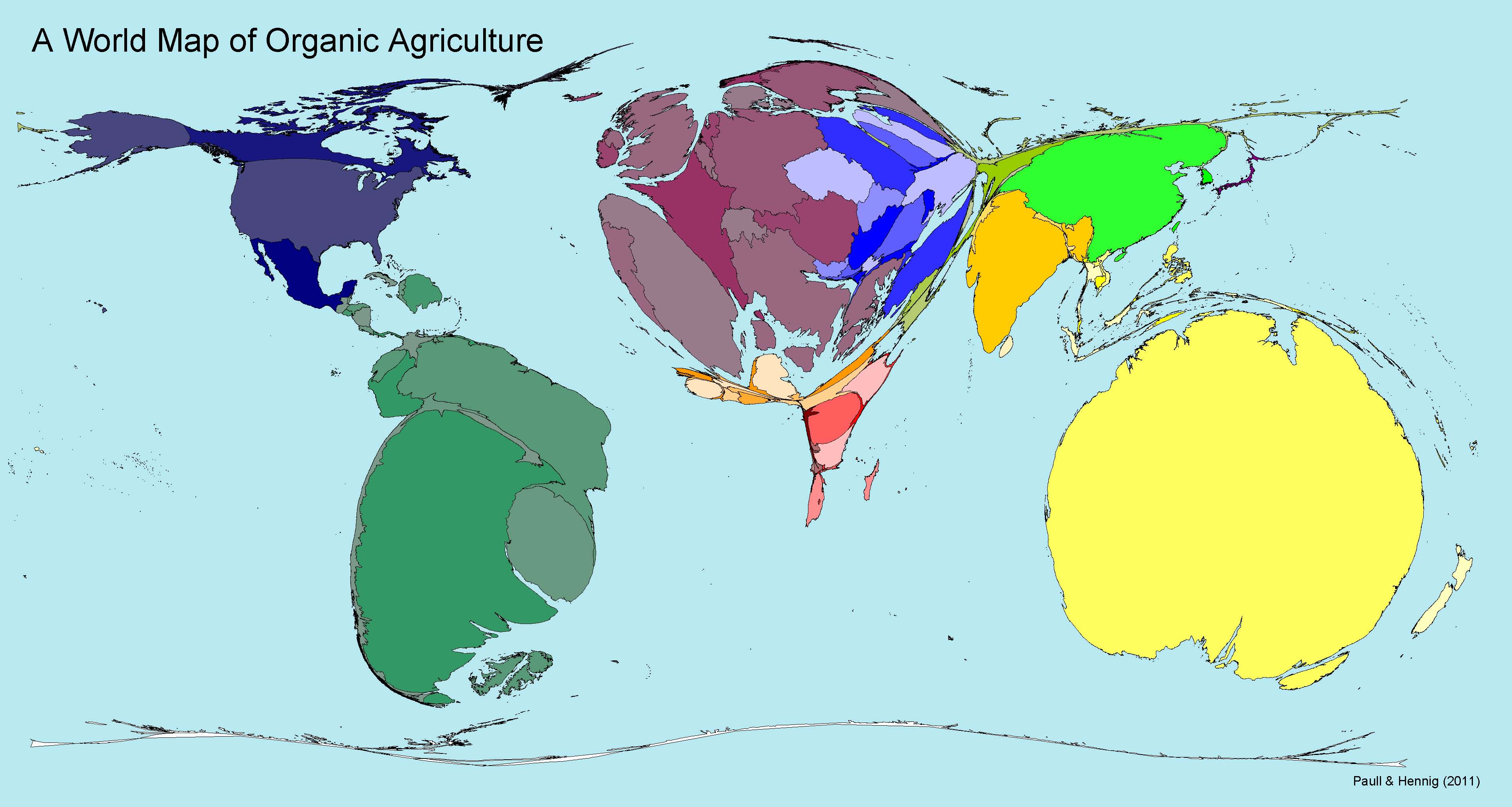
Робинсон придумал эту проекцию в 1963 году, сосредоточившись больше на «внешнем виде» карты, чем на точном измерении мест. Робинсон задумал карту, которая не является ни равновеликой, ни конформной, как инструмент общего назначения.
На самом деле, как он сказал New York Times в интервью 1988 года, «Я решил сделать это в обратном порядке. Я начал с своего рода художественного подхода. Я визуализировал самые красивые формы и размеры. Я работал с переменными до тех пор, пока не дошел до того, что если я изменил одну из них, то лучше не стало. Затем я вычислил математическую формулу для получения такого эффекта. Большинство картографов начинают с математики».
Надеюсь, эта карта заменит Меркатора в классах.
Плюсы: Показывает весь мир сразу
Минусы: Уступает как по площади, так и по углам, особенно на полюсах
Интересно: Какую карту использовал Христофор Колумб?
Винкель-Трипель
Предложенная немецким картографом Освальдом Винкелем в 1921 году проекция Винкеля-Трипеля является полной противоположностью проекции Робинсона.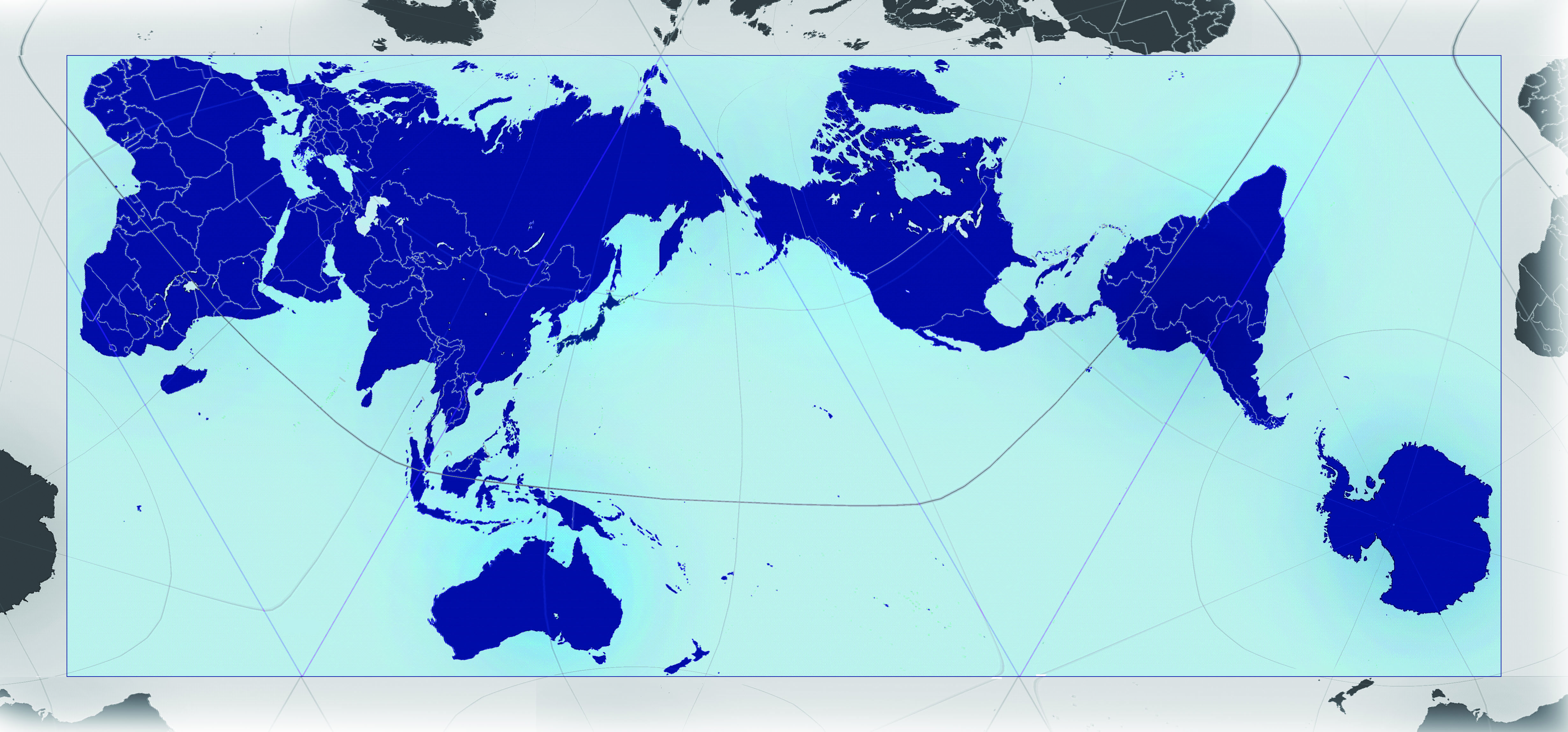
Карта прибегает к математике, чтобы сократить три основных типа искажений — площадь, направление и расстояние (отсюда и немецкий термин «тройной», Tripel, в названии). Эта проекция карты показывает, что Гренландия имеет тот же размер, что и Аргентина, а не всю Южную Америку.
Национальное географическое общество рисует все свои стандартные карты с использованием проекции Винкеля-Трипеля с 1998 года, и многие школы США последовали этому примеру. Однако, несмотря на свою популярность, поскольку карта не сохраняет углы, она и близко не заменит Меркатора в навигационных целях.
Плюсы: Достаточно точные формы и размеры стран
Минусы: Земли ближе к полюсам все еще увеличены
Обязательно к просмотру: Эти 5 инструментов позволят вам освоить картографические проекции
AuthaGraph
Это самая точная из существующих картографических проекций. На самом деле карта мира AuthaGraph настолько совершенна в пропорциях, что волшебным образом складывается в трехмерный глобус.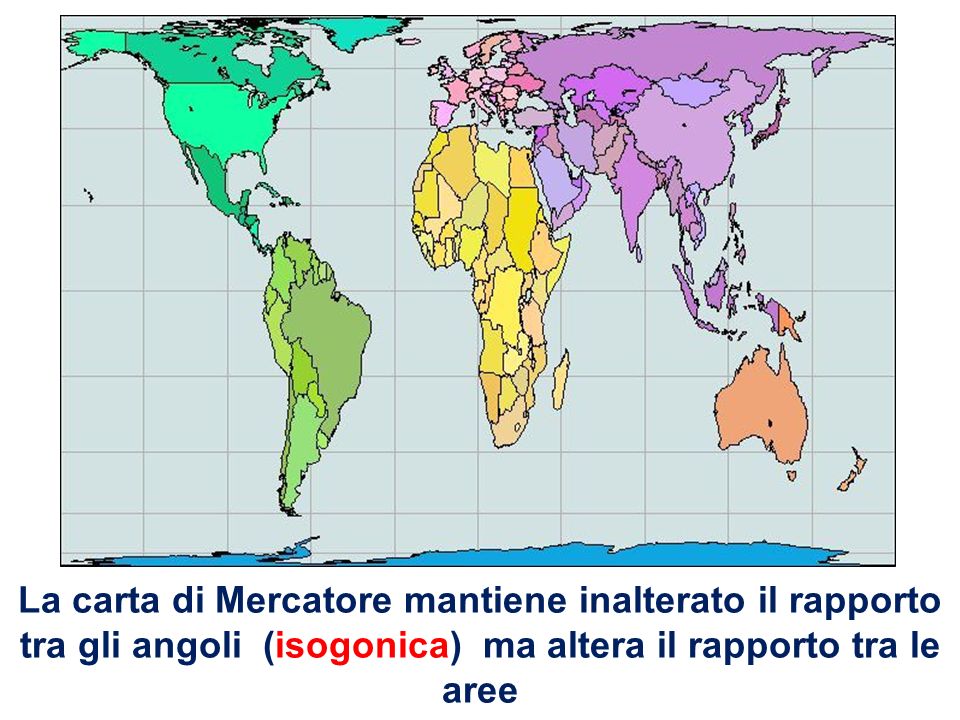
Японский архитектор Хадзиме Нарукава изобрел эту проекцию в 1999 году, разделив сферическую поверхность поровну на 96 треугольников. Затем эти треугольники были спроецированы на тетраэдр, что не только помогло сохранить пропорции земли и воды, но и помогло развернуть карту в идеальный плоский прямоугольник. Нарукава, однако, настаивает на , что если карта будет усовершенствована еще на шаг, чтобы увеличить количество подразделений, ее точность улучшится, и ее можно будет официально назвать картой равной площади.
Тем не менее, AuthaGraph реалистично представляет все океаны и континенты, включая заброшенную Антарктиду. И пока общая форма континентов сохраняется, вы заметите, что их ориентация перекошена вверх — как бы в улыбке!
Плюсы: Самый точный; принесет вам самую большую награду в области дизайна в Японии; можно сложить в 3D-глобус
Минусы: Полярный круг несколько раздавливается
Вашей любимой картографической проекции нет в списке? Дайте нам знать в комментариях ниже!
Принстонские астрофизики переосмысливают карту мира, разрабатывая менее искаженный, «радикально иной» взгляд на мир
Воспроизвести видео: Воспроизвести видео: Двусторонняя карта Земли Принстонские профессора Дж.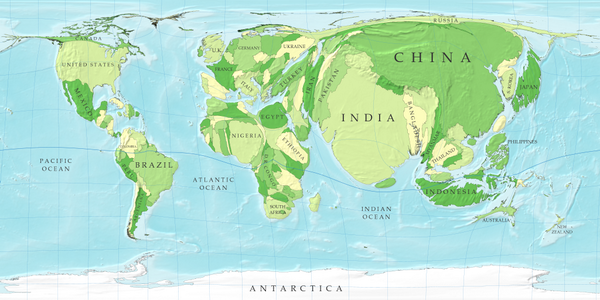
Ричард Готт а Роберт Вандербей работал с профессором Drexel Дэвидом Голдбергом над созданием революционно новой карты: двустороннего диска, который можно вставить в учебник или аккуратно сложить для хранения. Она обеспечивает более точные расстояния, чем любая существующая плоская карта, с минимальными визуальными искажениями.
Видео Дж. Ричарда Готта, Роберта Вандербея и Дэвида Голдберга
На протяжении веков картографы бились над тем, как точно отобразить нашу круглую планету на чем-либо, кроме глобуса.
Теперь фундаментальное переосмысление того, как могут работать карты, привело к созданию самой точной плоской карты из когда-либо созданных тремя экспертами по картам: Дж. Ричардом Готтом, почетным профессором астрофизики в Принстоне и создателем логарифмической карты. о вселенной, однажды описанной как «возможно, самая умопомрачительная карта на сегодняшний день»; Роберт Вандербей, профессор исследования операций и финансового инжиниринга, создавший карту результатов выборов «Фиолетовая Америка»; и Дэвид Голдберг, профессор физики Университета Дрекселя.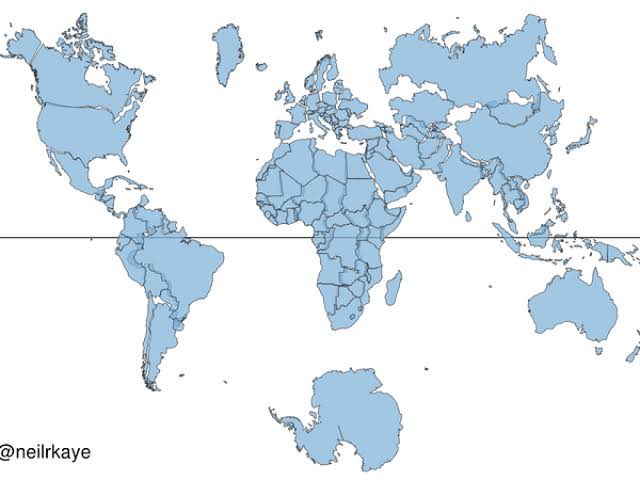
Их новая карта двусторонняя и круглая, как грампластинка или виниловая пластинка. Как и многие радикальные события, задним числом это кажется очевидным. Почему , а не имеют двустороннюю карту, которая показывает обе стороны земного шара? Он вырывается за рамки двух измерений, не теряя при этом логистического удобства — хранения и изготовления — плоской карты.
— Эту карту можно держать в руке, — сказал Готт.
В 2007 году Голдберг и Готт изобрели систему для оценки существующих карт, количественно определяя шесть типов искажений, которые могут вносить плоские карты: локальные формы, площади, расстояния, изгиб (изгиб), асимметрия (перекос) и граничные разрезы (разрывы непрерывности). ). Чем ниже оценка, тем лучше: глобус будет иметь оценку 0,0.
«Невозможно сделать все идеально», — сказал Готт, который также является выпускником Принстона 1973 года. «Карта, которая хороша в чем-то одном, может быть неэффективна в изображении других вещей». Проекция Меркатора, популярная на стенах классных комнат и используемая в качестве основы для карт Google, превосходно изображает локальные формы, но она так сильно искажает области поверхности вблизи Северного и Южного полюсов, что полярные области обычно просто обрезаются.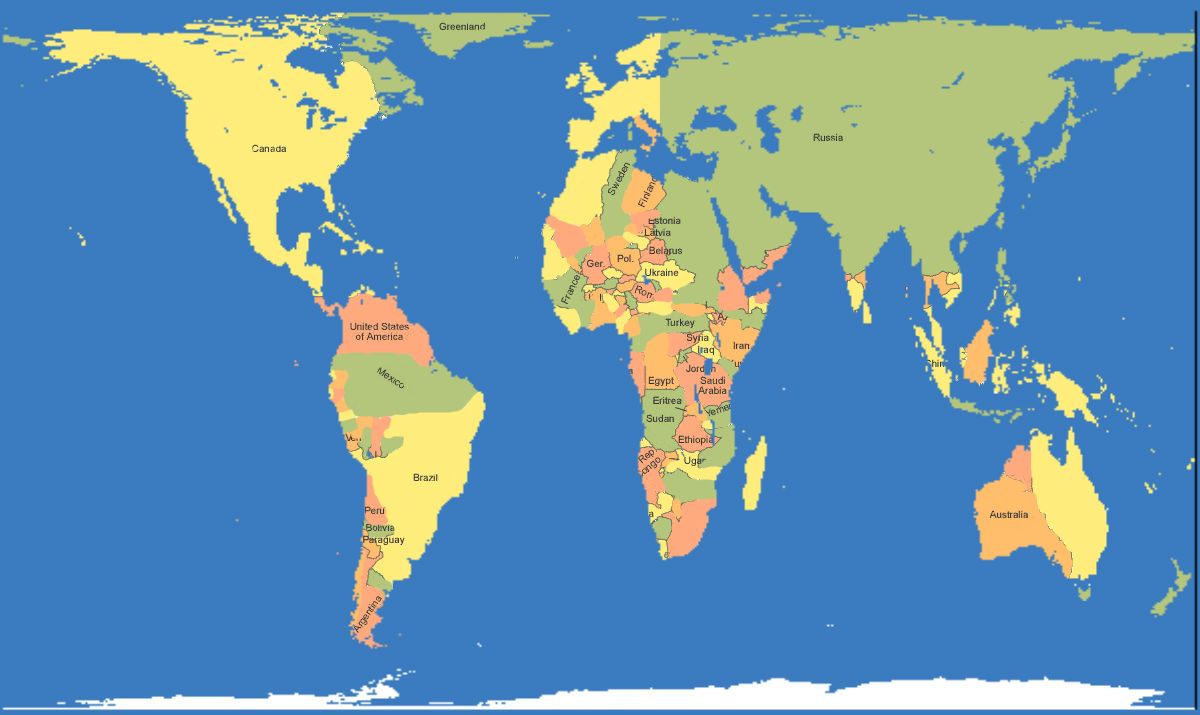
В проекции Меркатора полярные районы полностью искажены — Антарктида выглядит больше, чем все остальные континенты вместе взятые — и расстояния вводят в заблуждение: Япония и Гавайи выглядят очень далеко друг от друга. В системе, разработанной Голдбергом и Готтом для количественной оценки ошибок карты, где более низкие числа представляют меньшее искажение, проекция Меркатора получает 8,29 балла.6.
Карта Даниэля Р. Стребе через Wikimedia Commons
Используя их метрики, самой известной ранее плоской картографической проекцией был треугольник Винкеля с оценкой Голдберга-Готта 4,563. Но у этого все еще была проблема «разрезания границ», разделяющая Тихий океан и создающая иллюзию большого расстояния между Азией и Гавайями.
Проекция Winkel Tripel, выбранная National Geographic для своих карт мира, представляет полюса более точно, чем проекция Меркатора, но она все же сильно искажает Антарктиду и создает иллюзию, что Япония находится значительно восточнее Калифорнии, а не ближайшей к ней сосед с запада.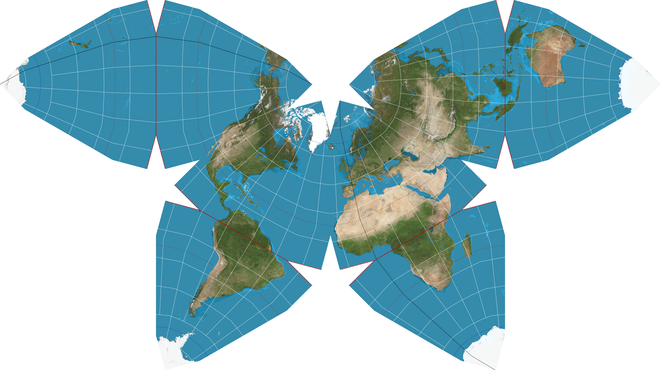
Оценка Гольдберга-Готта: 4,563
Карта Даниэля Р. Стребе с Wikimedia Commons
Очевидно, нужен был совершенно новый подход. Готт провел сравнение с олимпийскими прыгунами в высоту: в 1968 году Дик Фосбери шокировал любителей спорта, выгнув спину и прыгнув через перекладину назад. Он установил новый рекорд и выиграл золотую медаль, и с тех пор прыгуны в высоту прыгают назад.
— Мы как мистер Фосбери, — сказал Готт. «Мы делаем это, чтобы побить рекорд, сделать плоскую карту с наименьшей возможной ошибкой. Так что, как и он, мы удивляем людей. Мы предлагаем совершенно другой тип карты и превзошли Винкеля Трипеля по каждой из шести ошибок».
Вдохновение пришло из работы Готта о многогранниках — объемных многогранных фигурах.
В многогранных картах нет ничего нового — в 1943 году Бакминстер Фуллер разбил мир на правильные формы и дал инструкции, как сложить его и собрать в виде многогранного глобуса — но, хотя он мог защитить формы континентов, Фуллер раздробил океаны и увеличили многие расстояния, например, между Австралией и Антарктидой.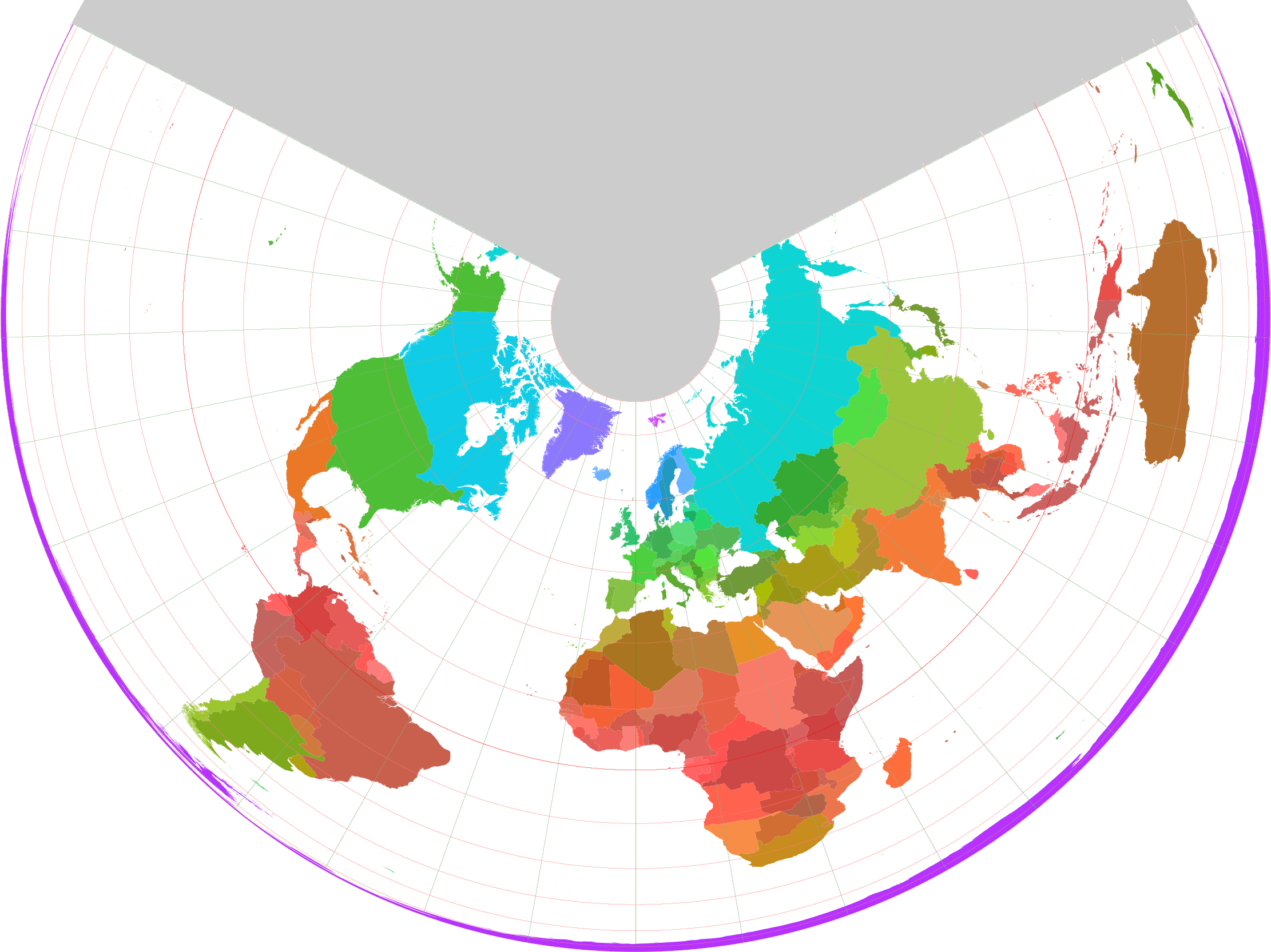
Бакминстер Фуллер популяризировал многогранную проекцию «Димаксион», основанную на развернутом икосаэдре. Антарктида «круглая, как и должно быть», сказал Готт, но эта проекция «разбивает» океаны. Оценка Гольдберга-Готта: больше 15
Изображение предоставлено Земной обсерваторией НАСА, с изменениями, внесенными Mapthematics LLC. карта.
Он может отображаться с восточным и западным полушариями с двух сторон или, в предпочитаемой Готтом ориентации, с северным и южным полушариями, что удобно позволяет экватору проходить по краю. В любом случае, это карта без границ. Он предположил, что для измерения расстояний от одной стороны до другой можно использовать веревку или измерительную ленту, протянувшуюся от одной стороны диска до другой.
«Если вы муравей, вы можете переползти с одной стороны этой «граммофонной пластинки» на другую, — сказал Готт. «У нас есть непрерывность над экватором. Африка и Южная Америка накинуты на край, как простыня на бельевую веревку, но они непрерывны».
Эта двусторонняя карта имеет меньшие ошибки расстояния, чем любая односторонняя плоская карта — предыдущим рекордсменом была карта 2007 года, составленная Готтом совместно с Чарльзом Муньоло, выпускником Принстона 2005 года. Фактически, эта карта замечательна тем, что имеет верхнюю границу ошибок расстояния: невозможно, чтобы расстояния отличались более чем на ± 22,2%. Для сравнения, в проекциях Меркатора и Винкеля, а также в других проекциях ошибки расстояния становятся огромными по мере приближения к полюсам и практически бесконечными слева направо (которые далеко друг от друга на карте, но непосредственно примыкают к земному шару). Кроме того, площади на краю всего в 1,57 раза больше, чем в центре.
Революционная двухсторонняя карта диска Готта, Голдберга и Вандербей сводит к минимуму все шесть типов искажений карты. Они использовали эквидистантную азимутальную проекцию: компромиссную проекцию, такую как треугольник Винкеля, с небольшими ошибками как в локальных формах, так и в областях, вместо оптимизации одной за счет другой.
Антарктида и Австралия представлены более точно, чем на большинстве других карт, а расстояния через океаны или полюса точны и их легко измерить, в отличие от односторонних плоских карт. Оценка ошибки Гольдберга-Готта: 0,881
Карта Дж. Ричарда Готта, Роберта Вандербея и Дэвида Голдберга.
Карта может быть распечатана на одной журнальной странице, и читатель может ее вырезать. Три картографа представляют себе, как они печатают свои карты на картоне или пластике, а затем складывают их стопкой, как пластинки, и хранят вместе в коробке или вкладывают в обложки учебников.
— В тонкую коробку можно поместить плоские двусторонние карты всех основных планет и лун Солнечной системы, — сказал Готт, — или стопку карт Земли с физическими данными, политическими границами, плотностью населения, климатом, языками. путешествия исследователей, империи в разные исторические периоды или континенты в разные геологические эпохи».
Насколько им известно, никто еще не делал двусторонних карт с такой точностью.