от ноты До к ноте Си
Термин Нота происходит с латинского языка и дословно переводится как Знак или другой вариант перевода — Метка. Понятие музыкальных нот тесно сопряжено с музыкальной нотацией. Если говорят Нота, в большинстве случаев имеют в виду её графической отображение на нотном стане, нотация простыми словами. В большинстве случаев ноты записываются на пяти линейной тактовой сетке. Что интересно данная система обозначения нот в музыке, а именно на 5 линейках, берет своё зарождение с 17 века.
Содержание
Нотная грамота для начинающих — советы новичкам по обучению музыкальной теории
Итак, нотами музыканты пытаются обозначить звук, представить его в виде понятных символов, которые живут по своему закону – закону чувств и ощущений. За любой нотой можно проследить её характеристики, а именно:
- высоту;
- длительность;
- порядок воспроизведения и законы взаимодействия с другими нотами.
Наверное, самая известная нота – это До. Или Ля. Принято считать, что звучание ноты Ля имеет эталонную частоту в 440 Гц.
Или Ля. Принято считать, что звучание ноты Ля имеет эталонную частоту в 440 Гц.
Ноты в музыке — всего 7 нот, но сколько песен
Действительно, казалось бы нотных вариаций должно не так много, однако на самом деле мелодий, что можно сочинить — бесконечность. Можете попробовать просчитать количество вариантов математически, их будет не меньше, чем в шахматах. Поэтому для игры музыки на музыкальных инструментах необходимо чувствовать, чтобы ориентироваться во всём этом многообразии звуков и их оттенков. Если вам трудно самостоятельно осваивать музыкальную теорию, обратитесь к репетитору, вы можете найти лучших гитаристов учителей на нашем официальном сайте Гитары.
C (нота До)
Частота: 261,6 Гц
Цвет: красный
Ступень звукоряда: 1
Английское обозначение: C
Пример звучания ноты До на гитаре:
Как найти ноту До на гитаре:
Как пишется нота До на нотном стане:
Где находится нота До на фортепиано:
Примечание: Далее все ноты идут последовательно белые клавиши: после До – Ре, Ми, Фа, Соль, Ля, Си.
Интересные факты о ноте До: «Дабы ослабевшими» — если вы не знаете, что означает нота До, то она означает именно это. Дабы ослабевшими переводится на латынь как Ut queant laxis и является 1-й строчкой гимна Иоанну Крестителю. Чтобы не говорить Ut queant laxis, принято краткое обозначение ноты До — (Ut), на русском языке произносится как «Ут». Особенность звучания гимна заключается в том, что тон каждой последующей строчки выше предыдущей, ровно на 1 тон. Это так называемый мнемонический прием под названием Гвидонов слог. Нота Ут была переименована во всем известное нотное обозначение До в 17 веке.
D (нота Ре)
Частота: 293,7 Гц
Цвет: Оранжевый
Ступень звукоряда: 2
Английское обозначение: D
Пример звучания ноты Ре на гитаре:
Как найти ноту Ре на гитаре:
Как пишется нота Ре на нотном стане:
Интересный факт:
Теория Сольфеджио гласит о том, что ноты — это мнемонические обозначения в музыкальных звукорядах. А звукоряд – это восходящие или нисходящие последовательности звуков. Сольмизация и сольфеджио являются терминами-синонимами. Говоря снова о гимне Иоанна Крестителя и вспоминая его строки, в частности вторую, мы найдём ноту Ре, а точнее resonare fibris. Так начинается вторая строчка того же гимна, что само словосочетание resonare fibris означает дословно – «Голосовыми связками». Вот именно первый слог второй строчки гимна и послужил для сокращенного названия ноты Ре.
А звукоряд – это восходящие или нисходящие последовательности звуков. Сольмизация и сольфеджио являются терминами-синонимами. Говоря снова о гимне Иоанна Крестителя и вспоминая его строки, в частности вторую, мы найдём ноту Ре, а точнее resonare fibris. Так начинается вторая строчка того же гимна, что само словосочетание resonare fibris означает дословно – «Голосовыми связками». Вот именно первый слог второй строчки гимна и послужил для сокращенного названия ноты Ре.
E (нота Ми)
Частота: 329,6 Гц
Цвет: Желтый
Ступень звукоряда: 3
Английское обозначение: E
Пример звучания ноты Ми на гитаре:
Как найти ноту Ми на гитаре:
Как пишется нота Ми на нотном стане:
Интересный факт: mira gestorum чудеса прославляет. Переводится третья строчка mira gestorum, всё того же гимна как «Чудеса прославить». Именно благодаря этому нота Ми получила своё сокращение в названии.
Именно благодаря этому нота Ми получила своё сокращение в названии.
F (нота Фа)
Частота: 349,2 Гц
Цвет: Зелёный
Ступень звукоряда: 4
Английское обозначение: F
Пример звучания ноты Фа на гитаре:
Как найти ноту Фа на гитаре:
Как пишется нота Фа на нотном стане:
Интересный факт: по старой доброй традиции, первый слог, начало 4-й строчки известного уже гимна послужил сокращенным названием для ноты Фа. Famuli tuorum переводится как «Деяний твоих». Кстати для тех, кто хочет послушать как именно звучит данный гимн Иоанну Крестителю, включите аудио:
А также послушайте инструментальный вариант исполнения гимна:
G (нота Соль)
Частота: 392 ГцЦвет: Голубой
Ступень звукоряда: 5
Английское обозначение: G
Пример звучания ноты Соль на гитаре:
Как найти ноту Соль на гитаре:
Как пишется нота Соль на нотном стане:
Интересный факт:
Solve polluti – данная строчка гимна переводится как «Очисти скверну» и является пятой по счету. Кстати для тех, кто хочет полностью лицезреть текст данного гимна, представляем его ниже:
Кстати для тех, кто хочет полностью лицезреть текст данного гимна, представляем его ниже:
Оригинал текста:
Ut queant laxis
Resonare fibris,
Mira gestorum
Famuli tuorum,
Solve polluti
Labii reatum,
Sancte Johannes
A (нота Ля)
Частота: 440 ГцЦвет: Синий
Ступень звукоряда: 6
Английское обозначение: A
Пример звучания ноты Ля на гитаре:
Как найти ноту Ля на гитаре:
Как пишется нота Ля на нотном стане:
Интересный факт:
Labii reatum – перевод 6-ой по счету строчки обозреваемого гимна есть «Устен нечистых». К слову перевести строчки слов с латыни можно не только дословно, но и по смыслу. И это пробовали сделать не один человек. Самые известные варианты перевода представлены ниже.
Перевод гимна Иоанна Крестителя на русский язык:
Версия 1 — Р.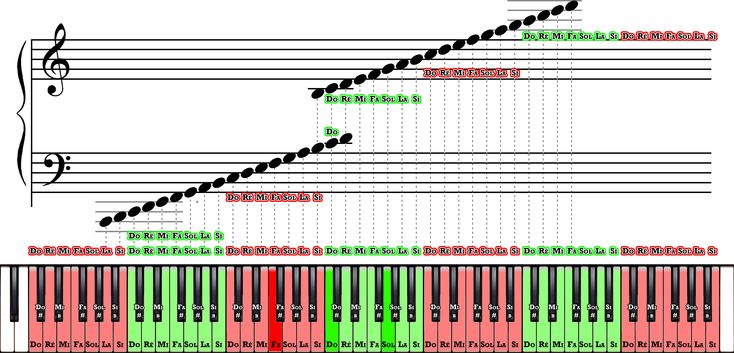 Л. Поспелова
Л. Поспелова
Чтобы открытыми устами
Смогли воспеть рабы
Твоих деяний чудеса,
Вину с порочных губ ты отпусти,
Святой наш Иоанн.
Версия 2 — С. Н. Лебедева
Чтобы рабы [твои] в полный голос
Могли воспеть чудеса твоих деяний,
Отпусти им, святой Иоанне, грех изустный.
Версия 3 — Н. П. Дилецкий
Да возможем хвалити чудеса,
Боже наш,
святых Твоих раби Твои,
развяжи устен скверных
прегрешения узы
Версия 4 — М. И. Катунян (мнемонический вариант перевода)
Утробою отверстой чтобы
Ревнители твои сумели
Миру возгласить деяний чудеса
Фальшь совлеки с их губ,
Солгать дабы не смели,
Лаская слух напевом,
Святый Иоанне. (Си)
H (нота Си)
Частота: 494 Гц
Цвет: Фиолетовый
Ступень звукоряда: 7
Английское обозначение: H
Пример звучания ноты Си на гитаре:
Как найти ноту Си на гитаре:
Как пишется нота Си на нотном стане:
Интересный факт:
Последняя строка гимна под названием «Ut queant laxis» – это Sancte Iohannes, что в переводе означает упоминание самого святого — Святый Иоанне. Данный гимн имеет обозначение нот в виде квадратов, а также современную нотацию, обе показаны ниже.
Данный гимн имеет обозначение нот в виде квадратов, а также современную нотацию, обе показаны ниже.
Квадратная нотация:
Современная нотация:
Ноты на гитаре для начинающих — популярные песни и музыка
Ноты для гитары для начинающих гитаристов порой запомнить не просто. Однако не невозможно, чтобы запомнить ноты, их названия и в каком месте они находятся на гитарном грифе, необходимо базовое знание теории и немного практики игры. Ноты для начинающих с нуля гитаристов всё же, считаю, будут нести не первостепенное значение для понимания гитары. Гораздо важнее на первом этапе обучения игры на гитаре обратить внимание на Аккорды и Ритм. А также, возможно, вам пора познакомиться с табулатурами.
В любом случае в музыке, как говорится, всего 7 нот, и знать их нужно; наверное, все их и так знают, но не понятно, как с ними работать, чтобы извлекать из них нужный звук. Для того существуют системы и принципы обращения с нотами. А именно как читать ноты, как их записывать, как образуются ноты разной длины, сколько нотных обозначений формируют полный такт в музыкальном произведении и так далее.
Чтобы эффективно играть на гитаре не обязательно знать ноты, но важно понимать основные принципы игры на инструменте, именно гитаре, тогда всё будет в порядке. Что нужно знать о нотах и нотной грамоте, будет полезно ознакомиться:
1. Размер. Три четверти, четыре четверти – это пример размерностей.
2. Такт. От одной вертикальной черты до другой.
3. Длительности. Восьмые, шестнадцатые, целые, половинные, и тд.
4. Доли. Сильная доля, слабая доля.
5. Громкость. Тише, громче.
6. Тембр. В зависимости от инструмента или особенностей голоса, если речь идет о вокале.
7. Звукоряд. Ноты До, ре, Ми, Фа, Соль, Ля, Си.
8. Бемоль, Диез, Бекар. Знаки альтерации повышают и понижают звучание нот.
Виды диезных и бемольных тональностей:
Диезные тональности
| Тональность (Мажор и минор) | Ключевые знаки |
| До мажор и ля минор | |
| Соль мажор и ми минор | |
| Ре мажор и си минор | |
| Ля мажор и фа-диез минор | |
| Ми мажор и до-диез минор | |
| Си мажор и соль-диез минор | |
| Фа-диез мажор и ре-диез минор | |
| До-диез мажор и ля-диез минор |
Бемольные тональности
| Тональность (Мажор и минор) | Ключевые знаки |
| До мажор и ля минор | |
| Фа мажор и ре минор | |
| Си-бемоль мажор и соль минор | |
| Ми-бемоль мажор и до минор | |
| Ля-бемоль мажор и фа минор | |
| Ре-бемоль мажор и си-бемоль минор | |
| Соль-бемоль мажор и ми-бемоль минор | |
| До-бемоль мажор и ля-бемоль минор |
9. Паузы. Как говориться давайте делать паузы в нотах.
Паузы. Как говориться давайте делать паузы в нотах.
Читайте подробнее что такое тональность и для чего она нужна.
Важны ли так ноты и нотная грамота на самом деле?
Разобрали поверхностно, что такое нотная грамота и как пишутся ноты на нотном стане. С помощью знания нот на гитаре или любом другом инструменте можно играть с умом, что по сути является музыкально грамотно. Учитесь музыке, записывайтесь на уроки игры на гитаре с нуля.
Число, лежащее в основе современной музыки / Хабр
Почему двенадцать?
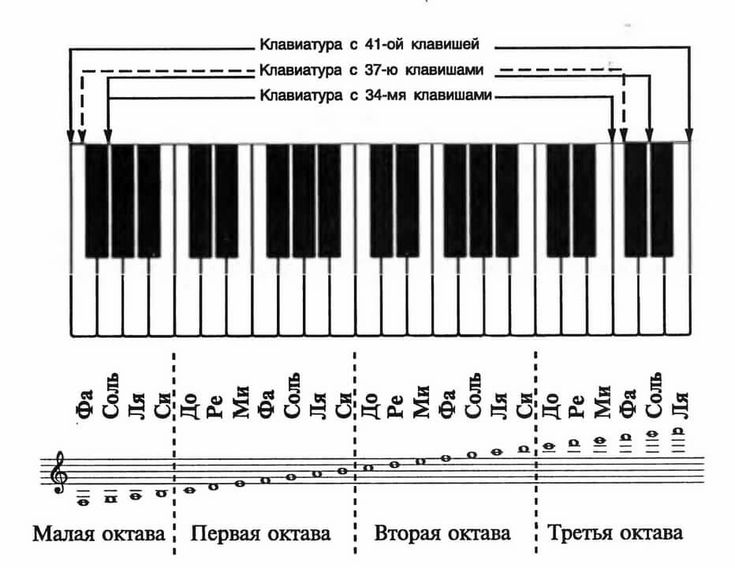
Если вы посмотрите на клавиатуру, то увидите, что в каждой октаве содержится 12 полутонов.
В случае фортепиано это всего лишь значит, что между, например, «до» первой октавы и «до» второй октавы расположено 11 клавиш. Вместе с одним из «до» (например, до второй октавы) мы получим 12 клавиш: до#, ре, ре#, ми, фа, фа#, соль, соль#, ля, ля#, си, до.
Но почему 12?
Может быть это просто случайность? Вот нравилось нашим предкам число 12, у них везде 12: 12 месяцев, 12 знаков зодиака, 12 колен Израилевых, 12 апостолов,… и здесь решили, пусть будет 12, и так и повелось. Или все же здесь есть объективный закон, и это число не случайно?
Или все же здесь есть объективный закон, и это число не случайно?
В этой статье я попытаюсь продемонстрировать, что это не случайность. Достаточно общие требования, вполне естественные для современной (западной) музыки, с математической необходимостью приводят нас к числу 12. Интересно, что причиной почему у нас появляется это значение является свойство другого числа (см. в конце статьи). Можно даже сказать, что оно то и лежит в основе современного звучания.
Постановка задачи
Сначала давайте попробуем формализовать задачу.
У нас есть опорная частота . Будем называть ее тоникой. У нас также есть октава с частотой . Теперь мы должны понять, какие могут быть варианты промежуточных частот от до , такие, чтобы мелодия, построенная на этих нотах, звучала бы для нашего слуха гармонично?
Боюсь, что эта формулировка, хотя и отражает суть вопроса, все же, с математической точки зрения, является довольно туманной, и на такой вопрос не может быть однозначного ответа, хотя бы потому, что человеческий слух имеет довольно ограниченную разрешающую способность по частоте. И это подтверждается тем, что в разное время использовались разные строи, например, пифагоров, чистый, хорошо темперированный, равномерно темперированный строи. И все они звучали и звучат, как минимум для определенных произведений, вполне приемлемо.
И это подтверждается тем, что в разное время использовались разные строи, например, пифагоров, чистый, хорошо темперированный, равномерно темперированный строи. И все они звучали и звучат, как минимум для определенных произведений, вполне приемлемо.
Что такое гармония?
Мы должны наложить некоторые дополнительные условия. Но прежде мы должны ответить на один важный вопрос: что мы воспринимаем как гармоничное звучание?
Давайте рассмотрим два звука — с частотами и .
Возьмем отношение этих частот. Это отношение можно представить в виде произведения чисел , где — простые числа, а — целые числа, например, это отношение может равняться . И чем эти простые числа () меньше, тем гармоничнее для нашего уха будет звучать этот интервал (я нашел это утверждение тут (см. второй абзац))
Так, например, самым гармоничным звучанием в соответствии с этим утверждением будет являться октава (изменение частоты в 2 раза). А следующими по гармоничности интервалами будут квинта (изменение частоты в раза) и кварта (изменение частоты в раза).
Но не так все просто с этим утверждением. Так, например, не очень понятно, как влияет степень. Например, что гармоничнее умножение на или на 7? Я не знаю, изучен этот вопрос или нет, и можно ли в принципе дать на него ответ. Также восприятие гармоничности — вещь довольно субъективная. Так, современная музыка полна звучаний, которые 100 — 200 лет были бы восприняты не иначе как жуткая какофония.
Условие первое. Тоника, кварта, квинта, октава
Эта неопределенность не является проблемой для нашего маленького исследования. Дело в том, что единственный вывод, который я хочу сделать из этого утверждения заключается в том, что в нашем строе в любом случае должны быть как минимум «самые гармоничные» интервалы, а именно, октава, кварта и квинта. То есть наряду с тоникой с частотой и октавой с частотой у нас также должны быть квинта и кварта, с частотами соответственно , или что-то очень близкое, что мы не смогли бы отличить от чистой квинты и кварты.
Замечание: на самом деле достаточно только тоники, квинты и октавы. Наличие квинты сразу дает нам и кварту, как дополнение до октавы, и в силу второго условия (инвариантность), которое описано ниже, мы также должны иметь кварту и от тоники. То есть необходимость наличия кварты есть следствие наличия квинты и требования инвариантности.
Наличие квинты сразу дает нам и кварту, как дополнение до октавы, и в силу второго условия (инвариантность), которое описано ниже, мы также должны иметь кварту и от тоники. То есть необходимость наличия кварты есть следствие наличия квинты и требования инвариантности.
И это наше первое требование.
Условие второе. Инвариантность
Вторым нашим требованием будет инвариантность. И это важное требование современной музыки. Заключается это требование в том, что все гармонии в любых тональностях должны звучать одинаково. Если мы говорим про современный строй, который применяется при настройке фортепиано, то это значит, что квинта, состоящая из семи полутонов, должна звучать одинаково, независимо от того, от какого звука она построена. То есть соотношение частот между до и соль должно быть таким же как и для до# — соль#, ре — ля, ре# — ля#,… и равняться . И эта инвариантность должна относиться, конечно, не только к квинте, но и к любым интервалам. Важным преимуществом этого строя является возможность транспонирования пьесы на любой интервал. В этом и заключается суть равномерной темперации.
В этом и заключается суть равномерной темперации.
Нужно сказать, что это требование инвариантности не является таким очевидным, и данный подход был применен относительно недавно, лишь в 18 веке. Строи, применявшиеся до этого, (например, пифагоров и чистый) не обладали таким свойством. Вот послушайте, например, Sonata for Microtonal Piano (Ben Johnston), написанную в чистом строе (prime limit = 5). Такое ощущение, что фортепиано не настроено. Все богатство современных гармоний основано именно на этой инвариантности. Например, «Хорошо темперированный клавир» Баха появился именно благодаря новому подходу в настройке клавишных. Именно вот эта инвариантность дала возможность Баху создавать гармонические последовательности, которые просто были невозможны раньше.
Итак, теперь мы имеем все необходимые для расчета данные.
Расчет
Давайте построим звукоряд от тоники до октавы, который бы удовлетворял обоим требованиям.
Предположим, что в этом случае мы получим звуков (включая октаву). Это и является искомым числом. Мы хотим показать, что при наших условиях должно равняться 12.
Это и является искомым числом. Мы хотим показать, что при наших условиях должно равняться 12.
Следствием второго требования является то, что интервал между частотами соседних звуков должен быть одинаковым и должен быть равен .
Теперь первое требование говорит о том, что в нашем ряду должны быть два звука, соответствующие (с хорошим приближением) частотам и . Это квинта и кварта. Предположим, что кварта это -ый звук в нашем ряду, а квинта — -ой. Обозначим .
Нетрудно видеть, что изменение частоты между квартой и квинтой (отношение частот) равно .
Но, в соответствии с нашим вторым условием, это также должно быть равно .
Итак, мы получили формулу:
После несложных преобразований получим основную формулу:
Легко увидеть, что решением (конечно, приблизительным) является , где — любое натурально число (достаточно малое, потому что все же 0,170 отличается от 1/6).
Давайте рассмотрим случай . В этом случае , . То есть, это вариант современного строя, только без полутонов, только с тонами (до, ре, ми, фа#, соль#, ля#, до). Но, как вы видите, в этом случае кварта (фа) и квинта (соль) в этот звукоряд не попали.
Но, как вы видите, в этом случае кварта (фа) и квинта (соль) в этот звукоряд не попали.
То есть единственным вариантом для нас может быть
, где — любое натурально число ( достаточно малое). Случай как раз и соответствует нашему современному строю, который называется равномерно темперированный строй.
Но почему не 24 или большее число? Причина проста — могу предположить, что такая градуированность уже является излишней для нашего восприятия. Поэтому остается только одно число: 12.
Если вас не устраивают приведенный ход мысли, то здесь вы можете найти
строгое математическое доказательство
Задача:
Найти минимальное натуральное число N, при котором найдется натуральное число такое, что отличается от не более, чем на центов.
Решение:
Обозначим через . Тогда, при (что справедливо для диапазона тех и , которые мы будем рассматривать) наша задача сводится к нахождению минимального , при котором
,
где — функция округление до ближайшего целого.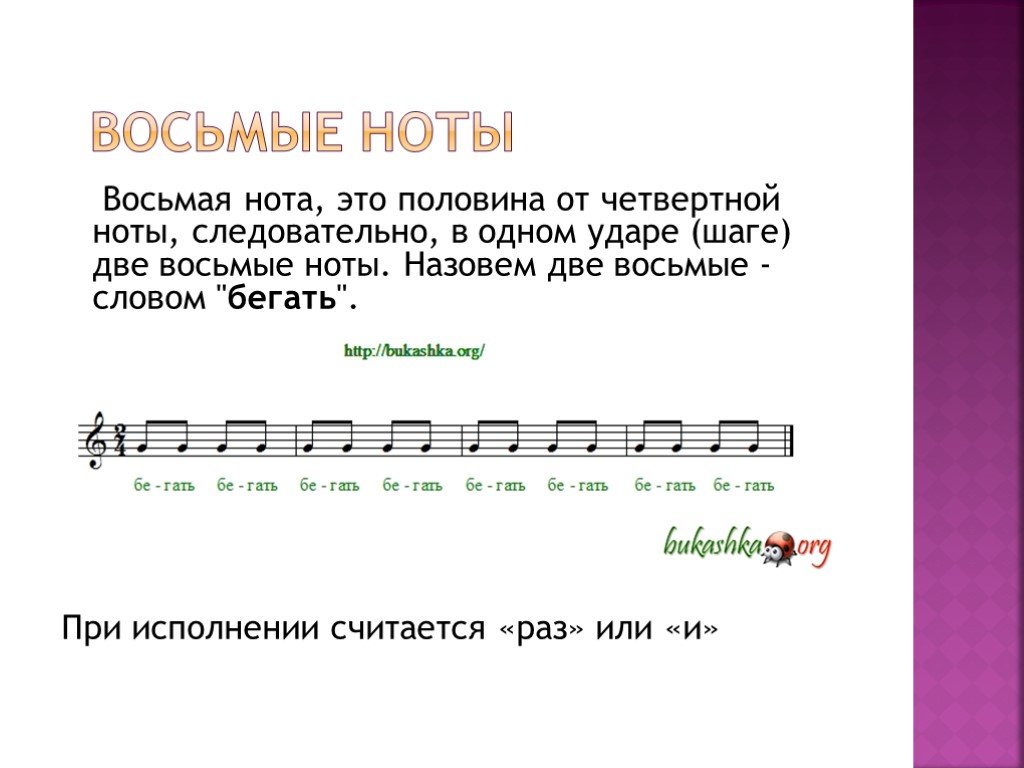
Будем решать эту задачу численно.
Теперь самое время все же определиться с .
Какую величину (в центах) несоответствия чистой квинты и «нашей» квинты мы считаем приемлемой? Многие слышат, например, то что большая/малая терция в равномерно темперированном строе «фальшивит». А ведь это всего лишь около 15 центов по отношению к чистым интервалам. Поэтому наше требование должно быть лучше, чем 15 центов. Некоторые источники говорят, что на определенных частотах музыканты различают до 5 — 6 центов. Поэтому разумно взять .
Тогда из таблицы однозначно видно, что наименьшее . Следующие «удовлетворительные» .
Замечание:
Следующей итерацией, для каждого нужно так же проверять звучания и других интервалов. В случае , например, терции становятся совсем «фальшивыми»: больше 30 центов (для большой терции).
Таким образом наш ответ: . Что и требовалось доказать.
И, кстати, видно, что наш ответ не изменится, если мы вместо взять, например, 10 или даже 15.
Заключение. Число, лежащее в основе
Удивительно, но получается, что числом, лежащим в основе современного музыкального строя и современной (европейской) музыки, является , а именно то, что с хорошей точностью (0,1%) выполняется следующее равенство:
Ответы на замечания и критику в комментариях
Прежде всего спасибо за интересные комментарии!
Здесь мои ответы на наиболее важные (на мой взгляд) замечания и критику.
Критика 1. Яйцо или курица
Druu: Смотрите, 12 звуков в октаве было до равномерной темперации вообще, поэтому вы не можете обосновывать 12 звуков при помощи темперации, это будет просто неверно заведомо.
lair: Это именно та кольцевая логика, про которую я и говорю: если выбрать музыку, построенную на определенном строе, очевидно, что в ее контексте другой строй невозможен.
На эти и похожие замечание я бы привел 2 контраргумента:
1) если бы с достаточной точностью не выполнялось бы равенство , то невозможно было бы «натянуть» равномерно темперированный строй на чистый строй, состоящий из 12 звуков. Чем сильнее отличался бы от , тем фальшивее звучала бы наша квинта. Если это число было бы (сильно) другим, то не было бы равномерно темперированного приближения к чистым интервалам, и, как следствие, не было бы современной музыки или, скажем так, она была бы другой. Поэтому вполне логичен вывод о том, что свойства числа лежат в основе современной музыки.
Чем сильнее отличался бы от , тем фальшивее звучала бы наша квинта. Если это число было бы (сильно) другим, то не было бы равномерно темперированного приближения к чистым интервалам, и, как следствие, не было бы современной музыки или, скажем так, она была бы другой. Поэтому вполне логичен вывод о том, что свойства числа лежат в основе современной музыки.
2) второй контраргумент невозможно строго логически обосновать, и является лишь предположением, но мне кажется, что все же это рассуждение достойно внимания. Давайте попробуем ответить на вопрос, а почему вообще возникла потребность в равномерно темперированном строе? В комментариях уже отчасти был дан ответ. Музыка в то время (время создания равномерно темперированного строя) уже использовала модуляции и полифонии, которые на самом деле, по большому счету, уже требовали равномерной темперации. Проблема «фальшивого» звучания решалась тем, что музыканты чуть «подстраивали» звучание во время исполнения. Это легко было сделать для струнных (во всяком случае безладовых), духовых и для вокала (поправьте, если я не прав — этот вывод я сделал из ваших комментариев). Например, для скрипки — это всего лишь легкое изменение положения пальцев. Но как только вы были лишены такой возможности (клавесин), то сразу все начинало звучать плохо. Итак, все выглядит так, что вот эти 12 нот появились не просто так, а как естественное развитие музыки в сторону вот этой возможности свободных модуляций и богатых полифоний, а это в свою очередь является следствием инвариантности. Это было естественное развитие музыки. То есть я хочу сказать, что если бы математически инвариантность была бы возможна не для 12 звуков, а, например, для 10, то мы бы (еще до равномерной темперации) в нашем звукоряде имели бы 10 звуков (в данном случае я говорю о пути развития европейкой музыки). А потом бы «натянули» 10 звуков равномерной темперации на наш чистый строй.
Например, для скрипки — это всего лишь легкое изменение положения пальцев. Но как только вы были лишены такой возможности (клавесин), то сразу все начинало звучать плохо. Итак, все выглядит так, что вот эти 12 нот появились не просто так, а как естественное развитие музыки в сторону вот этой возможности свободных модуляций и богатых полифоний, а это в свою очередь является следствием инвариантности. Это было естественное развитие музыки. То есть я хочу сказать, что если бы математически инвариантность была бы возможна не для 12 звуков, а, например, для 10, то мы бы (еще до равномерной темперации) в нашем звукоряде имели бы 10 звуков (в данном случае я говорю о пути развития европейкой музыки). А потом бы «натянули» 10 звуков равномерной темперации на наш чистый строй.
Критика 2. Уникальность двенадцати
Очень много было критики по поводу утверждения, что 12 — это единственное разумное число.
Во-первых, понимая агрессивность этого утверждения и в принципе невозможности строгого обоснования, я по-возможности снизил степень категоричности некоторых утверждений в статье. И все же…
И все же…
В данном случае имеем 2 линии критики.
1) Почему я считаю, что 19, 24 или 29 (и т.д.) неприемлемы?
Нет, не считаю. Для разных инструментов существуют приемы использования звуков за пределами звукоряда, например, глиссандо и вибрато. Эти приемы придают красоту и естественность звучанию. Поэтому, даже с 12-ю нотами мы и сейчас используем вспомогательные звуки. Если мы говорим об антураже, о необычном звучании, об обогащении звучания…, то это вполне оправдано, но если мы говорим об основных тонах, то здесь у меня сомнения. Музыка создается не только для избранных, а для обычных людей, и вот для них такая градуированность (ИМХО) является излишней.
Второй аргумент, и он был приведен в комментариях, заключается, действительно, в сложности создания инструментов и исполнения в случае длинного звукоряда, хотя, у нас есть прекрасный пример такого инструмента — ситар. Но попробуйте взять на пианино октаву (одной рукой), если у вас будет звукоряд из 24 звуков.
2) А как же пентатоника?
Во всех восточных странах, в которых я был, я почему-то очень редко слышал национальную музыку, построенную на пентатонике. И все музыканты с востока, которых я слушал (а некоторых люблю), тоже исполняли вполне европейскую музыку. Вот интересная цитата: «Академические композиторы начиная с XIX века применяли пентатонику как особую краску для придания музыке аромата архаики «. Аромат архаики…
В моем восприятии все же эта музыка не является современной, но не хочу отстаивать эту позицию, поэтому в некоторых местах в статье использую термин «современная европейская музыка». Ясно, что эта музыка (построенная на пентатонике) развивалась по другим законам, и не дошла до требования богатой полифонии и частой и легкой модуляции, которые проявились в европейской музыки. Поэтому эта статья очевидно не про пентатонику.
Критика 3. Современная музыка
Что я называю современной музыкой?
Хотя это и выглядит тавтологией, но под современной музыкой я подразумеваю музыку, которая требует инвариантности, что в случае инструментов с фиксированным строем (например, клавесин, пианино) приводит к необходимости равномерно темперированного строя (или чего-то близкого). В случае остальных инструментов, например, безладовых струнных, все выглядит несколько сложнее, потому что, в действительности, есть возможность использовать больший (чем 12) набор звуков. Но все же, когда мы говорим про требование инвариантности, то подразумеваем, что эти звуки должны быть очень близкими (по частоте) к нашим 12.
В случае остальных инструментов, например, безладовых струнных, все выглядит несколько сложнее, потому что, в действительности, есть возможность использовать больший (чем 12) набор звуков. Но все же, когда мы говорим про требование инвариантности, то подразумеваем, что эти звуки должны быть очень близкими (по частоте) к нашим 12.
В это определение входит почти вся фортепианная музыка, европейская классическая, джазовая, рок музыка, попса и все производные от них. Уверен, что есть исключения, но ИМХО это именно исключения. Спорить об этом не вижу смысла, т.к. каждый может вкладывать в это понятие что-то свое.
Критика 4. Расчет
Ошибка в расчетах.
Думаю, этот вопрос снят. Впрочем, должен признать, что в процессе дискуссии мною было сделано несколько ошибочных утверждений о второстепенных вещах, которые не повлияли на основной вывод статьи.
P.S. Не стоит относиться к этой статье (и предъявлять соответствующие требования), как к академическому труду. 🙂 Это не статья по теории музыки. Тем более это не статья по истории музыки. В этих областях я ни в коей мере не считаю свое знание хоть сколько-нибудь значительным и допускаю, что могут быть неточности, хотя и старался их избегать. Здесь сформулирована простая математическая задача (школьного уровня сложности), решение которой, как мне показалось, имеет интересную интерпретацию. С чем я и поделился.
🙂 Это не статья по теории музыки. Тем более это не статья по истории музыки. В этих областях я ни в коей мере не считаю свое знание хоть сколько-нибудь значительным и допускаю, что могут быть неточности, хотя и старался их избегать. Здесь сформулирована простая математическая задача (школьного уровня сложности), решение которой, как мне показалось, имеет интересную интерпретацию. С чем я и поделился.
Где в октаве 12 нот?
Гитара-концентратор
Одна вещь, которую многие музыканты считают само собой разумеющейся, — это выбор , который мы делаем, чтобы разделить октаву на 12 равных частей.
На самом деле, многие музыканты не понимают, что это выбор. Вот насколько эта идея воспринимается как должное.
Но потенциальных произведений в октаве гораздо больше 12. И многие системы настройки были использованы или предложены, начиная с 12-тональной системы, которую мы используем, и заканчивая системами, которые делят октаву более чем на 50 нот.
В этой области существует небольшое сообщество композиторов, исполнителей и исследователей. Однако развитие микротональной музыки, тона которой меньше, чем 12 произведений, которые мы обычно используем, идет медленно. Возможно, причина в том, что большинство инструментов рассчитано на 12-тональную октаву. Но теперь публика обучена слышать и ценить 12-тональную музыку. Также относительно мало музыкантов, создающих микротональную музыку. И хотя 12-тональная система является стандартной, системы, использующие более 12 нот, являются экспериментальными и не так хорошо изучены. Использование любой другой системы делает вас пионером. Наконец, люди, наиболее заинтересованные в создании микротональной музыки, как правило, не заинтересованы в том, чтобы сделать музыку более созвучной. Они склонны видеть потенциал для создания необычных и передовых звуков. Таким образом, у микротональной музыки есть проблема с рекламой, потому что ее наиболее опытные исполнители являются рекламой новинки, а не музыки мейнстрима.
Немного истории
Сотни лет назад, до того, как у нас появились инструменты для измерения музыкального звука, не было достаточной основы для понимания того, как работают музыкальные звуки. По этой причине, хотя люди потенциально могли петь богатые гармонии без специального оборудования, концепция развивалась медленно, и в старинной музыке гармония была относительно простой.
Многие ранние инструменты, особенно человеческий голос и струнные инструменты без ладов, такие как скрипка, могли воспроизводить любую высоту звука в пределах октавы. Но с появлением инструментов с жестко «фиксированной» высотой звука, особенно фортепиано (и гитары), возникла необходимость в разработке системы точного определения того, какой будет эта высота звука.
Для создания инструментов, на которых можно играть вместе, возникла необходимость в универсальной системе настройки.
Однако, чтобы разработать общепризнанную систему настройки, пришлось пойти на множество компромиссов. Некоторые люди даже считают, что эти компромиссы нанесли серьезный ущерб музыке. В нашем современном мире все музыкальные инструменты и оборудование основаны на 12-тональной системе. Но что, если в самой чисто звучащей музыке 19 нот или 22? Или 51?
Некоторые люди даже считают, что эти компромиссы нанесли серьезный ущерб музыке. В нашем современном мире все музыкальные инструменты и оборудование основаны на 12-тональной системе. Но что, если в самой чисто звучащей музыке 19 нот или 22? Или 51?
Масштаб (практически бесконечный)?
Чтобы понять различные возможности деления октавы, нам нужно использовать некоторую единицу измерения, чтобы говорить о различиях частот между разными тонами в пределах октавы.
В музыке термин центов используется для описания разницы в высоте звука. В октаве 1200 центов, поэтому в нашей 12-тональной гамме, состоящей из нот, расположенных через равные промежутки, каждая нота отстоит на 100 центов друг от друга. Эта единица измерения равна относительно и полезна только для сравнения. При необходимости частоту можно использовать для измерения абсолютных значений высоты тона.
Но что, если наши банкноты отличаются друг от друга на 50 центов? Тогда у нас была бы гамма с 24 нотами, и она звучала бы совсем по-другому.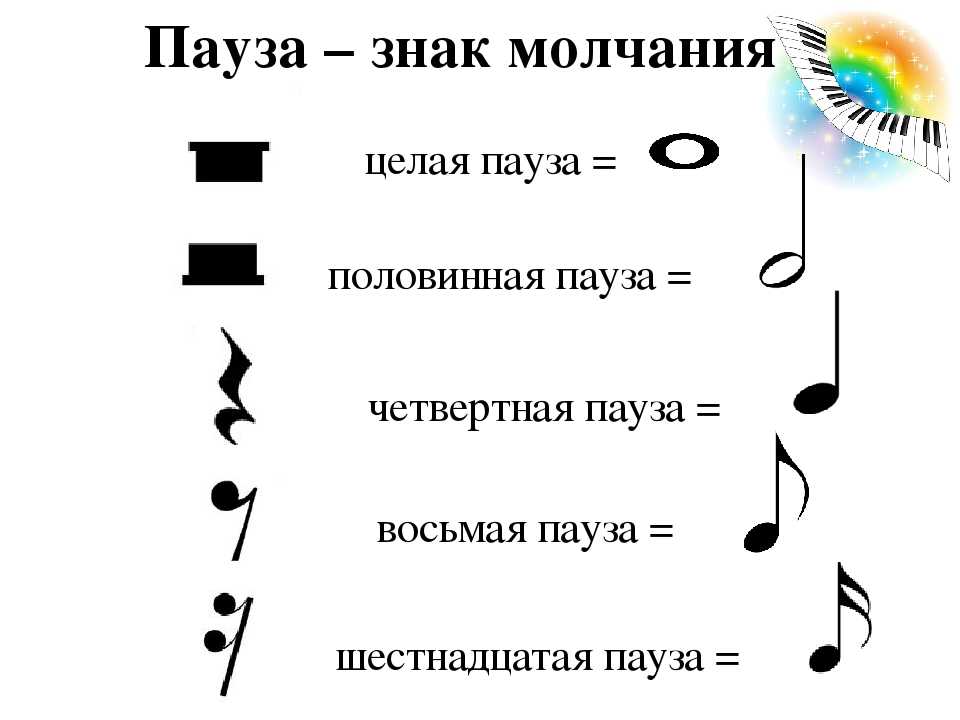
Для этого обсуждения мы предлагаем новую единицу измерения, называемую P зуд A слышимый D различение, или PAD. Один PAD равен 5 центам. Это потому, что 5 центов — это приблизительная разница в высоте тона, необходимая среднему человеку для обнаружения разницы между двумя тонами. Поскольку любые другие высоты тона могут оказаться ниже способности восприятия среднего человека, мы ограничим наше обсуждение только теми приращениями тона, которые можно обнаружить. Итак, октава состоит из 240 PAD с, а одна нота в нашей 12-тональной системе состоит из 20 PAD с.
Основа гармонии
Наиболее важным понятием для понимания гармонии является знание того, как две ноты сочетаются друг с другом. Подумайте вот о чем: возьмите любую ноту случайным образом и используйте ее в качестве основного тона. Теперь добавьте вторую, более высокую ноту к первой, чтобы гармонизировать ее. Полученную гармонию лучше всего представить как деление длины волны; сколько раз вибрация этой второй волны будет вибрировать в промежутке первой. Это то, что определяет созвучие и диссонанс, и так создается гармония. Люди, вероятно, уже открыли самые важные гармонии. Хотя есть музыканты, работающие с более чем 12 нотами, этот урок касается этих основных 12 нот, почему они существуют и как они настраиваются.
Это то, что определяет созвучие и диссонанс, и так создается гармония. Люди, вероятно, уже открыли самые важные гармонии. Хотя есть музыканты, работающие с более чем 12 нотами, этот урок касается этих основных 12 нот, почему они существуют и как они настраиваются.
Нижняя буква «С» будет точкой отсчета. Остальные примечания заключены в кавычки, поскольку, как вы увидите, их определение не является фиксированным.
Возьмите тон под названием «средний до» и произведите гармонически совершенный мажорный аккорд.
Как вы помните, одна нота в нашей 12-тональной системе равна 20 пэдам. Тот факт, что «настоящая» мажорная терция выше C составляет 76 PAD, а не 80, означает, что наша 12-тональная система неточно представляет эту ноту. Это немного не так. Это потому, что наша система темперировал или регулировал так, чтобы все 12 нот были точно равны друг другу. Хотя большая терция в нашей системе не совсем верна, идеальная квинта в основном верна. (Каждая чистая квинта в 12-TET почти точно настроена на соотношение 3:2. Результат отличается менее чем на половину одного PAD, разница не заметна для большинства человеческих ушей.) Если мы решим настроить каждую E на фортепиано вверх на 4 пэда, теперь мажорная терция верна, но идеальная квинта от ля до ми будет неправильной. Темперамент — это компромисс, и никто не может быть полностью счастлив.
(Каждая чистая квинта в 12-TET почти точно настроена на соотношение 3:2. Результат отличается менее чем на половину одного PAD, разница не заметна для большинства человеческих ушей.) Если мы решим настроить каждую E на фортепиано вверх на 4 пэда, теперь мажорная терция верна, но идеальная квинта от ля до ми будет неправильной. Темперамент — это компромисс, и никто не может быть полностью счастлив.
Почему 12 нот?
Вся человеческая музыка основана на гармонии, которая, по-видимому, проистекает из естественных законов.
Например, спойте ноту «до». Попросите вашего друга спеть чистую квинту выше, или «соль». Теперь сыграйте те же две ноты на любом современном инструменте. Этот интервал, идеальная квинта, является самым сильным и наиболее согласным интервалом. Его соотношение частот составляет 3:2. Это означает, что G будет вибрировать с частотой три раза на каждые два раза, когда вибрирует C. И действительно, в нашей 12-тональной системе строя квинты представлены очень хорошо. Разница между истинно чистой квинтой (3:2) и квинтой в нашей системе настолько незначительна, что не превышает девятки.0029 ПОДУШКА . Поэтому 12-тональная система достаточно точно представляет этот интервал. Однако каждый интервал индивидуален. А некоторые интервалы настолько плохо представлены в 12-тональной системе, что фактически находятся на расстоянии 10 падов от той ноты, которой они должны быть. Расстояние между двумя нотами равно 20 пэдам. Таким образом, расхождение в 10 пэдов находится ровно посередине между двумя нотами, и это очень серьезно. Это означает, что интервал крайне неточен.
Разница между истинно чистой квинтой (3:2) и квинтой в нашей системе настолько незначительна, что не превышает девятки.0029 ПОДУШКА . Поэтому 12-тональная система достаточно точно представляет этот интервал. Однако каждый интервал индивидуален. А некоторые интервалы настолько плохо представлены в 12-тональной системе, что фактически находятся на расстоянии 10 падов от той ноты, которой они должны быть. Расстояние между двумя нотами равно 20 пэдам. Таким образом, расхождение в 10 пэдов находится ровно посередине между двумя нотами, и это очень серьезно. Это означает, что интервал крайне неточен.
Так почему же 12 купюр? В ходе истории люди устанавливали гармонии для любой данной ноты на основе второй ноты, соответствующей определенному соотношению первой. Открытие дебатов о том, сколько нот должно быть в октаве, не обязательно предполагают, что существует более 11 приятных способов гармонизировать одну ноту.
Сколько существует 12-нотных систем?
На протяжении всей истории было предложено много 12-нотных систем. Если вы действительно не хотите много узнать по этой теме, не слишком беспокойтесь о различиях между этими системами. Вот что вам нужно знать:
Если вы действительно не хотите много узнать по этой теме, не слишком беспокойтесь о различиях между этими системами. Вот что вам нужно знать:
- В современной гармонии обычно 12 нот в октаве
- Многие системы были разработаны для разделения октавы на 12 частей
- Поскольку примечания на самом деле основаны на соотношениях (делении небольших чисел), все системы неверны , поскольку ни одна из них не может точно представить 12 примечаний во всех ситуациях
- 12-Tone Equal Temperament, система деления октавы точно на 12 совершенно равных частей, выиграла битву и стала мировым стандартом
- Just Intonation относится к строю, в котором частота двух нот соответствует соотношению, которому они принадлежат, но математически невозможно, чтобы все 12 нот соответствовали 9.0080
Суммарный урон
Различия между нотами клавиши, сыгранной в 12-тональной равной темперации, могут быть недостаточно большими, чтобы беспокоить большинство людей. Но они начинают расширяться, если принять во внимание возможность повторения вычисления для другой банкноты.
Но они начинают расширяться, если принять во внимание возможность повторения вычисления для другой банкноты.
Учтите, что мы играем в тональности до мажор и играем ноту ми, которая, как мы знаем, уже на 4 пэда отстоит от своего истинного центра. Эта разница может быть незначительной. Но теперь мы хотим использовать эту ми как второстепенный доминантный аккорд V/VI. Поэтому мы повышаем его треть до G♯. Но источник G ♯ — это не нота 5: 4 над корнем, E. Она также одинаково темперирована. В E уже было четыре плоских нота, и теперь мы знаем, что каждая крупная терция в нашей системе — это четыре неточных падов. Таким образом, теперь новый G♯ фактически на 8 падов отличается от правильной ноты, которая соответствовала бы начальному тону, разрешающемуся в A. Когда мы рассматриваем этот тип накопления, мы можем увидеть большую проблему с равной темперированной настройкой.
Подводя итог , разницу между одинаковой темперацией и «истинными» нотами, которые он пытается приблизить, может быть нелегко услышать всего в одном или двух примерах. Но по ходу более длинного музыкального произведения оно станет четче и заметнее.
Но по ходу более длинного музыкального произведения оно станет четче и заметнее.
Примеры прослушивания
Вам может быть трудно услышать разницу, особенно на таком коротком примере. Если вы считаете, что файлы абсолютно одинаковы, попробуйте воспроизвести их оба одновременно. Тогда вы сможете услышать разницу.
C
дим7♭9 Хорда, 12-тетC
dim7♭9 Аккорд, простая интонацияC
maj7♯11 Аккорд, 12-TETC
maj7♯11 Аккорд, простая интонацияДополнительные примеры
- Сравнение трех систем настройки
- Демонстрация Acapella: Just Intonation vs. Equal Tuning
- Canon in D в 3 различных системах настройки
Сколько мелодий?
То же, что писатель смотрит на пустую страницу и думает, как ее заполнить, — это композитор, уставившийся на 88 черно-белых нот на фортепиано и задающийся вопросом, как сочинить мелодию, которую никто раньше не слышал. Как можно взять восемь нот стандартной гаммы и написать совершенно новую мелодию, когда уже написано так много замечательных мелодий? Возможно, их всех забрали!
Как можно взять восемь нот стандартной гаммы и написать совершенно новую мелодию, когда уже написано так много замечательных мелодий? Возможно, их всех забрали!
Сколько существует комбинаций?
Итак, чтобы развеять опасения по поводу отсутствия новых мелодий, я подумал, что было бы интересно изучить количество мелодий, доступных композитору, глядя на свой пустой нотоносец, чтобы увидеть, сколько их потенциально может быть.
Первое, что нужно сделать, это установить некоторые основные правила. Это:
- Мелодии будут единым потоком нот — никаких аккордов, контрмелодий или басовых партий — только одна музыкальная линия. Помните «старый тест на серый свисток»? Если ее можно сыграть на свистульке — это мелодия.
- В первом разделе я убрал ритм, чтобы сосредоточиться только на перестановках нот.
- Все мелодии должны содержаться в пределах октавы — от C до C’ включительно.
- Можно использовать любую из 13 хроматических нот октавы.
 Я не ограничивал это только мажорной или минорной гаммой, так как во многих великих мелодиях используется знаков альтерации (черные ноты в до-мажорной гамме). Таким образом, мы можем включить все ноты в пределах октавы, включая скачок октавы (от C к C’), иначе Over the Rainbow не будет считаться мелодией! Ноты: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C’.
Я не ограничивал это только мажорной или минорной гаммой, так как во многих великих мелодиях используется знаков альтерации (черные ноты в до-мажорной гамме). Таким образом, мы можем включить все ноты в пределах октавы, включая скачок октавы (от C к C’), иначе Over the Rainbow не будет считаться мелодией! Ноты: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C’.
Мы решим эту проблему, начав с самой простой из возможных мелодий, состоящей из двух нот, а затем увеличивая длину мелодии по одной ноте за раз, пока не увидим закономерность, которую можно превратить в формулу.
Мелодии из двух нот
Сколько мелодий из двух нот можно написать в октаве? This one is easy and all combinations can be written out:
| First note | Second note | Pitch difference (semitones) |
| С | С | 0 |
| С | С# | 1 |
| C | D | 2 |
| C | D# | 3 |
| C | E | 4 |
| C | F | 5 |
| C | F# | 6 |
| C | G | 7 |
| C | G# | 8 |
| C | A | 9 |
| C | A# | 10 |
| C | B | 11 |
| C | C’ | 12 |
| First note | Second note | Pitch difference (semitones) |
| C’ | C’ | 0 |
| C’ | B | -1 |
| C’ | A# | -2 |
| C’ | A | -3 |
| C’ | G# | -4 |
| C ‘ | G | -5 |
| C’ | F# | -6 |
| C’ | F | -7 |
| C’ | E | -8 |
| С’ | Д# | -9 |
| C’ | D | -10 |
| C’ | C# | -11 |
| C’ | C | -12 |
Теперь вам может быть интересно, почему не включены такие комбинации, как G# — F и E — A. Это потому, что нас интересует только относительная высота звука, а не абсолютная нота. Для целей этого упражнения мелодия C – C идентична D – D или G – G, поскольку все они представляют собой унисонных мелодий 9.0006 (т. е. у них 0 в качестве разницы высоты тона). Поэтому мы не будем считать унисонные мелодии C’-C’ — в первой таблице унисон уже был покрыт C-C.
Это потому, что нас интересует только относительная высота звука, а не абсолютная нота. Для целей этого упражнения мелодия C – C идентична D – D или G – G, поскольку все они представляют собой унисонных мелодий 9.0006 (т. е. у них 0 в качестве разницы высоты тона). Поэтому мы не будем считать унисонные мелодии C’-C’ — в первой таблице унисон уже был покрыт C-C.
Исключив C’-C’, мы имеем в общей сложности 25 захватывающих двухнотных мелодий!
Мелодии из трех нот
Количество мелодий из трех нот возрастает достаточно резко, но не настолько, чтобы их тоже нельзя было записать.
Небольшой отрывок из электронной таблицы, в которой перечислены все 2197 комбинаций из трех нот с дубликатами, выделенными серым цветом. Вы можете увидеть всю таблицу здесь.
Мы можем начать с перечисления всех возможных комбинаций из трех нот, а затем вычеркнуть повторяющиеся. Оказывается, найти дубликаты легко: это именно те последовательности нот, в которых нет ни одной буквы C. Любую мелодию без буквы «до» всегда можно переместить вниз по шкале, пока ее самая нижняя нота не станет «до». Следовательно, любая мелодия без «до» является дубликатом мелодии, содержащей «до». Чтобы сосчитать все мелодии, все, что нам нужно сделать, это для подсчета всех последовательностей нот, кроме C.
Любую мелодию без буквы «до» всегда можно переместить вниз по шкале, пока ее самая нижняя нота не станет «до». Следовательно, любая мелодия без «до» является дубликатом мелодии, содержащей «до». Чтобы сосчитать все мелодии, все, что нам нужно сделать, это для подсчета всех последовательностей нот, кроме C.
Существует ровно 2197 комбинаций из трех нот, из которых 1728 не содержат до. Таким образом, всего 2197 – 1728 = 469 трехнотных мелодий.
Неплохо!
От четырех до бесконечности
Теперь записывать все возможные комбинации нот и выбирать из них ноты с буквой «до» — не очень эффективный способ дальнейшего исследования, поэтому нам нужно уравнение, которое будет описывать увеличение количества мелодий. Предположим, мы считаем мелодии, составленные из нот (мы уже рассмотрели и ). Существует 13 вариантов того, какой может быть первая нота (от C до C’), 13 вариантов второй ноты и так далее. Это означает, что количество всех последовательностей нот равно 9.0007
Из этого нам нужно вычесть последовательности, в которых нет C. Для такой последовательности есть 12 вариантов для первой ноты, 12 вариантов для второй ноты и так далее. Таким образом, количество всех последовательностей нот, не содержащих до, равно
Для такой последовательности есть 12 вариантов для первой ноты, 12 вариантов для второй ноты и так далее. Таким образом, количество всех последовательностей нот, не содержащих до, равно
| . |
Что говорит нам о том, что количество последовательностей нот, содержащих до (количество мелодий), равно 9.0007
Мы можем пойти еще дальше и найти количество мелодий для любой гаммы. Если количество нот в гамме равно (в нашем случае ), то количество мелодий, содержащих ноты, равно
Но вернемся к нашему примеру с Подстановка все больших чисел вместо — длины мелодии — дает нам следующий ответ на наш первоначальный вопрос, количество потенциальных мелодий в пределах октавы:
| Length of melody | No of possible melodies |
| 2 | 25 |
| 3 | 469 |
| 4 | 7,825 |
| 5 | 122,461 |
| 6 | ок. 1,84 миллиона 1,84 миллиона |
| 7 | ок. 26,9 млн |
| 8 | ок. 385 миллионов |
| 9 | ок. 5,4 миллиарда |
| 10 | ок. 75 миллиардов |
Таким образом, простая мелодия из десяти нот произведет более 75 миллиардов потенциальных мелодий из 13 нот в пределах октавы! Нашему композитору потребуется некоторое время, чтобы разобраться с ними. Компьютеру было бы проще — если кто-нибудь создаст программу, которая циклически перебирает их все, сообщите нам об этом!
Внесите ритм
Было бы неплохо также учитывать ритм, просто чтобы быть законченным, так как очень немногие мелодии представляют собой последовательности нот одинаковой длины.
К счастью, это гораздо проще вычислить. Потенциально длина ноты может быть любой между полуквавером , (шестнадцатая нота) и полубревом , (целая нота). (Я обесцениваю полу-полукваверов !) Вместо того, чтобы включать каждую вариацию, я думаю, что это был бы разумный выбор нот, которые можно было бы использовать:
Это означает, что существует 8 различных возможных длин ноты. , и каждая новая нота, добавленная к последовательности, умножает количество комбинаций на 8. для последовательности нот формула, которая подсчитывает различные вариации ритма, проста, что дает нам окончательный расчет, как показано ниже:
, и каждая новая нота, добавленная к последовательности, умножает количество комбинаций на 8. для последовательности нот формула, которая подсчитывает различные вариации ритма, проста, что дает нам окончательный расчет, как показано ниже:
| Length of melody | No of possible note combinations | Rhythm variations (ignoring melodies) = 8 n | Number of melodies (note combinations multiplied by rhythm variations |
| 2 | 25 | 64 | 1600 |
| 3 | 469 | 512 | 240,128 |
| 4 | 7,825 | 4,096 | 32 million |
| 5 | 122,461 | 32,768 | 4 billion |
| 6 | ca. 1,84 миллиона | 262 144 | 4,8 x 10 11 |
| 7 | ок. 26,9 млн 26,9 млн | ок. 2,1 миллиона | ок. 5,6 x 10 13 |
| 8 | ок. 385 миллионов | ок. 16,8 млн | ок. 6,4 х 10 15 |
| 9 | ок. 5,4 миллиарда | ок. 1,3 x 10 8 | ок. 7,02 x 10 17 |
| 10 | ок. 75 миллиардов | ок. 1,1 x 10 9 | ок. 8,25 x 10 19 |
Или для последнего числа:
Существует около 82 500 000 000 000 000 000 мелодий длиной 10 нот.
Этого достаточно! Очень грубое приближение показывает, что этому материалу более 2,6 триллиона лет. И, как упоминалось в начале, это даже не начинает принимать во внимание вариации, предусмотренные гармонизацией, оркестровкой, темпом или небесами выше — внесение новой встречной мелодии!
Итак, я думаю, сообщение таково: нет никакого оправдания блоку писателей.
Об авторе
Оли Фреке — лондонский музыкант и композитор, который по-разному поддерживал Human League с электро-группой Cassette Electrik, написанной для телевидения, и недавно добился успеха в клубных чартах с треком Line-1.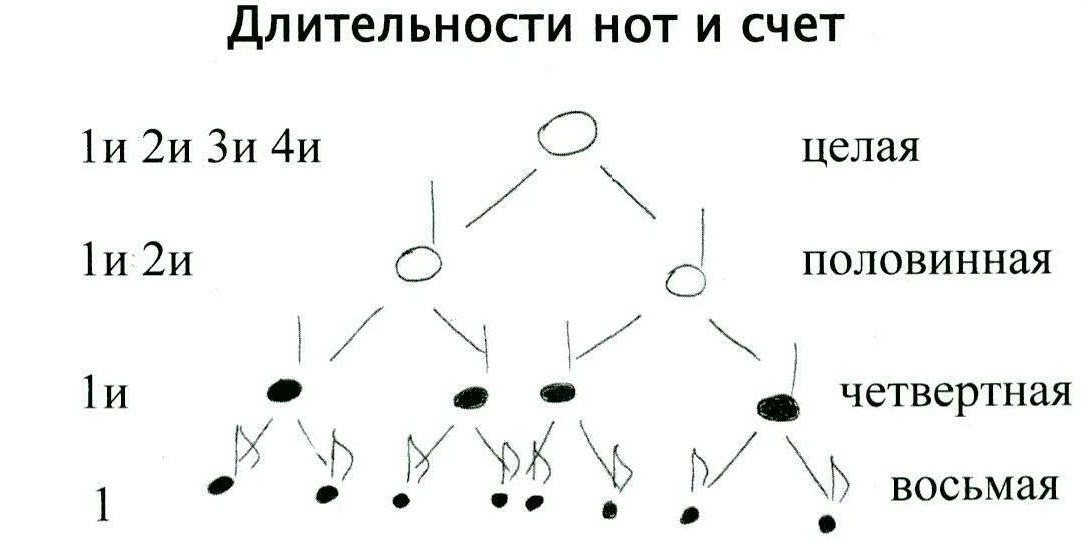

 Я не ограничивал это только мажорной или минорной гаммой, так как во многих великих мелодиях используется знаков альтерации (черные ноты в до-мажорной гамме). Таким образом, мы можем включить все ноты в пределах октавы, включая скачок октавы (от C к C’), иначе Over the Rainbow не будет считаться мелодией! Ноты: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C’.
Я не ограничивал это только мажорной или минорной гаммой, так как во многих великих мелодиях используется знаков альтерации (черные ноты в до-мажорной гамме). Таким образом, мы можем включить все ноты в пределах октавы, включая скачок октавы (от C к C’), иначе Over the Rainbow не будет считаться мелодией! Ноты: C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C’.