Интересное. Теория шести рукопожатий (после просмотра фильма «Ёлки»)
Теория шести рукопожатий (Six degrees of separation) — теория, согласно которой любые два человека на Земле разделены лишь шестью уровнями общих знакомых. Теория выдвинута в 1969 году психологами Стэнли Милгрэмом (Stanley Milgram) и Джеффри Трэверсом (Jeffrey Travers). Предложенная ими гипотеза заключалась в том, что каждый человек опосредованно знаком с любым другим жителем планеты через недлинную цепочку общих знакомых. В среднем эта цепочка состоит из шести человек.
Теория опиралась на данные эксперимента в двух американских городах. Они попросили около 300 человек в штате Небраска отправить письмо в Бостон, штат Массачусетс. Но не по почте, а через своих знакомых. Проследив пути этих писем, учёные пришли к выводу, что любых двух жителей вышеупомянутых штатов разделяют всего 6,2 «посредника».
Сотрудники компании Microsoft Эрик Горвиц (Eric Horvitz) и Юре Лешковец (Jure Leskovec) изучили пути следования 30 миллиардов мгновенных сообщений, отправленных с 240 миллионов компьютеров в июне 2006 года.
По оценкам авторов исследования, это составляет половину всех сообщений за рассматриваемый период. Получилось, что в среднем между любыми двумя получателями находятся 6,6 «звеньев», то есть общих знакомых.
В 1998 году аспирант Корнелльского университета Дункан Уоттс (по легенде, изучал взаимоотношения сверчков) решил ответить на вопрос: как одинокие сверчки находят самку? Дункану пришла идея об эксперименте на людях, потому что сверчки не очень охотно участвуют в экспериментах. Уоттс вспомнил о работах Милгрэма и предложил Стиву Строгацу с факультета прикладной и теоретической механики проверить, насколько тесен мир, еще раз.
Построенная ими компьютерная модель показала, что существуют «люди-шлюзы», в несколько раз укорачивающие цепочки между непересекаемыми сообществами. И даже небольшое их количество уменьшает количество уровней.
Очень интересный пример. Проверили на Голливуде. Анализ базы данных imdb.com показал, что голливудский мир действительно тесен: среднестатистический актер работал вместе с шестьюдесятью другими, и цепочка от одного к другому, в среднем, состоит не более чем из трех звеньев.
Актерские цепочки пронизывают не только пространство, но и время. Например, Кевина Бейкона отделяют от Чарли Чаплина всего три шага: сам Бейкон играл с Лоуренсом Фишберном, который играл с Марлоном Брандо, который снимался с Чаплином. Роль связующих звеньев в гильдии играют мастера, заставшие несколько кинематографических эпох (как Брандо), снимавшиеся в фильмах разных стран (как Брюс Ли, приехавший в Голливуд из Гонконга) и работающие в разных жанрах4 (как Мел Гибсон, снявшийся и в «Смертельном оружии», и в «Гамлете»).
Кульминацией нового исследования стало масштабное повторение эксперимента Милгрэма. Участие в эксперименте приняли 61168 добровольцев из 166 стран. Конечных адресатов было несколько — от американского профессора до эстонского архивариуса или норвежского ветеринара.
Успешные цепочки, в среднем, состояли из четырех звеньев. Исходя из этого, Уоттс и Строгац рассчитали среднюю длину гипотетической успешной цепочки, и результат совпал с результатами Милгрэма. Но из 24 тысяч писем, отправленных на первом этапе эксперимента, только 384 дошли до адресатов.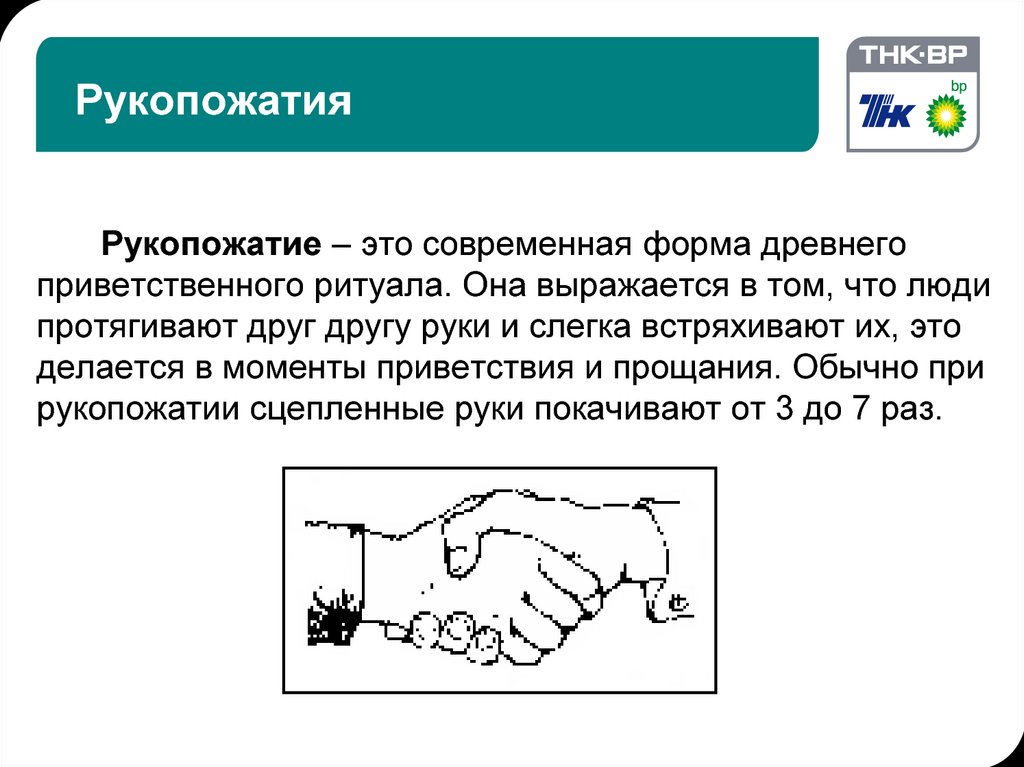
Почему же так мало писем добрались до адресата? Исследователи предположили, что это произошло по двум причинам. Во-первых, часть добровольцев потеряли интерес к эксперименту, что привело к обрыву многих цепочек. Во-вторых, многие просто не знали, кому отправить письмо, то есть не могли выбрать знакомого, который был бы ближе к адресату, чем они. «Если вам нужно, чтобы письмо дошло до Сибири, вы не думаете: «У кого из моих знакомых много друзей?», — говорит Уоттс. — Вы думаете: «Кто же из моих знакомых русский?».
Вывод был сделан парадоксальный: несмотря на то что правило шести звеньев, без сомнения, справедливо, на практике оно зачастую не работает, потому что мы не осведомлены в полной мере о возможностях собственного круга общения.
В научной статье это изложено так:
Возможно, тезис о том, что у большинства из нас довольно узкий круг общения, и что общество скрепляют сверхобщительные индивиды, кажется не слишком очевидным, однако это доказанный факт. Сети «малого мира» (а к ним относятся социальные сети или, например, интернет) характеризуются малым диаметром, высокой разреженностью вершин и склонны к кластеризации.
Другими словами, существует относительно немного ключевых вершин, оттягивающих на себя большую часть потоков, и множество вершин, которые связаны только с несколькими соседями. Плотность входящих и исходящих потоков описывается не пуассоновским распределением, а степенным законом.
Метки: жизнь, життя, интересное, наука, открытия, технологии, человек
Теория шести рукопожатий — Мастерок.жж.рф — LiveJournal
Если честно не особенно то я верю во все это, но такая теория есть.
Впервые идею о том, что любые два человека в мире могут быть соединены последовательностью личных контактов и что эта цепочка в большинстве случаев будет составлена из определенного числа (а именно — из пяти) звеньев, сформулировал венгерский писатель Фридеш Каринти. Его рассказ, написанный в 1929 году, так и назывался: «Звенья цепи». В рассказе шла речь о некой игре, мысленном эксперименте, имевшем целью доказать, что население Земли куда ближе друг к другу, чем принято считать. Выглядело это так: называли любого человека, знаменитого или неизвестного, из числа 1,5 млрд жителей Земли начала XX века, — и нужно было построить цепочку не более чем из пяти человек, соединяющих игрока с этим человеком.
Вот характерный отрывок из рассказа: «Хорошо, Сельма Лагерлеф, — сказал один из участников игры, — это проще простого». И уже через пару секунд он выдал решение: «Сельма Лагерлеф недавно получила Нобелевскую премию по литературе, так что она должна знать шведского короля Густава, он во время церемонии вручал ей награду. Широко известно, что король Густав любит играть в теннис и участвует в международных соревнованиях. Ему доводилось играть и с Белой Керлингом, так что они должны быть знакомы. Так получилось, что я тоже знаю Керлинга». (Говоривший сам был неплохим теннисистом.) «Для этого нам потребовалось два звена из пяти. И неудивительно, всегда проще найти кого-нибудь, кто знаком со знаменитостью, нежели с заурядной персоной. Ну, дайте-ка мне что-нибудь посложнее!»
Сегодня эта идея известна в русскоязычной части мира под названием «теории шести рукопожатий», по-английски же ее принято называть «теорией о шести рубежах отдаления».
Давайте узнаем про это подробнее …
Эксперименты, подтверждающие гипотезу
Однако без экспериментальных подтверждений это предположение остается не более чем игрой мысли.
И эксперименты неоднократно проводились. Сначала гипотезу о том, что все люди знакомы друг с другом через относительно небольшое число промежуточных связей, проверил известный американский психолог Стэнли Милгрэм. Эксперимент, поставленный в 1967 году, назывался «Тесный мир».
Триста человек участников, случайно выбранные жители двух городов- Омахи, штат Небраска, и Уичито, штат Канзас, — должны были отправить письма некоему биржевому брокеру в Бостоне. Адрес был неизвестен, однако можно было переслать письмо через кого-нибудь из знакомых, кто теоретически мог знать этого таинственного получателя, — и так далее, пока письмо не придет куда надо. Каждый промежуточный получатель-отправитель должен был дописать в письме свое имя, чтобы можно было проследить, как шло письмо и какой длины получилась цепочка. Когда подвели итоги эксперимента, оказалось, что средняя длина цепочки между первым отправителем и бостонским получателем — пять человек (или шесть связей — «рукопожатий»). В последующие годы подобные эксперименты проводились не раз, в разных условиях и с различными исходными данными.
Все они подтверждали гипотезу.
Так, например, двое исследователей из Корнеллского университета, Дункан Уоттс и Стивен Строгатц, в 1998 году создали математическую модель «тесного мира» и повторили эксперимент Милгрэма с большим размахом. В их эксперименте участвовали несколько десятков тысяч добровольцев со всего мира, и конечных точек было несколько — получатели жили в разных странах, в крупных городах и в относительной глубинке, были людьми разных занятий и из разных социальных слоев. В этом исследовании письма передавались уже не по почте и не из рук в руки, а через интернет. Результат был близок к результату Стэнли Милгрэма: средняя длина цепочки составила около шести звеньев. Кроме того, математическая модель показала некоторые интересные закономерности организации человеческих сообществ: например, что важную роль в глобальной коммуникации играют отдельные люди, принадлежащие одновременно к нескольким сообществам.
Наиболее же масштабное исследование, доказывающее гипотезу, провели в 2006 году Юре Лесковец и Эрик Хорвитц из компании Microsoft.
Они проанализировали логи службы мгновенных сообщений MSN Messenger- всего более 30 млрд сообщений, отправленных 240 млн человек за 30 дней (разумеется, вся эта статистика обсчитывалась не вручную, а на компьютере, и исследование заняло около двух лет). Не читая тексты сообщений, Лесковец и Хорвитц могли видеть данные пользователей: пол, возраст, местоположение, кто как часто общается, насколько объемны его сообщения и кто кого знает. Результаты этого исследования обширны, но главное, что нам интересно, — среднее расстояние между двумя пользователями MSN составило 6,6 связи. Это число больше, чем в эксперименте Милгрэма, но довольно близко к нему.
В социальной сети ВКонтакте приложение («Цепочка друзей — теория шести рукопожатий») позволяет искать цепочки знакомств между пользователями сети. Поскольку аудитория ВКонтакте ограничена (Россия и страны СНГ), добиться тех же результатов, какие были описаны выше, не удаётся — цепочки оказываются короче (3—4 человека). Однако интересно, что цепочки длиной более 6 человек практически не встречаются, что косвенно подтверждает изначальную теорию.
Вот тут подробнее про подобный эксперимент
С повсеместным распространением интернета принцип легкодоступности практически любого человека стал очевиден. В социальных сетях и крупных тематических сообществах — таких как LiveJournal, Facebook, VKontakte, Twitter и даже Wikipedia — существуют сервисы, позволяющие проследить цепочку общих знакомых от одного пользователя до другого, игры, основанные на принципах «тесного мира», и исследовательские приложения; есть и специальные сетевые проекты, созданные с целью дальнейшего исследования возможностей глобальной коммуникации.
По данным самого свежего эксперимента на эту тему, сегодня любого можно найти через социальные сети всего за 12 часов. Это стало известным благодаря Алексу Резерфорду из Масдарского института науки и технологий в Абу-Даби и социальной игре Tag Challenge, проведенной в 2012 году.
Целью соревнования было отыскать пять человек в пяти разных городах США и Европы. Единственными зацепками были фотоснимок человека, название города, в котором он находится, и информация о том, что он одет в футболку с логотипом Tag Challenge.
Команда Алекса Резерфорда выиграла соревнование, разыскав трех из пяти человек в течение всего 12 часов.
Вопреки традиционной в таких ситуациях стратегии – рассказать об объекте поисков как можно большему количеству разных людей – команда Алекса Резерфорда пошла по другому пути, обращаясь персонально к тем, кто может помочь в поисках, основываясь на географических данных и другой информации, доступной в социальных сетях. По мнению руководителя команды, вполне вероятно, что при правильном подходе найти нужного человека можно и быстрее.
И все-таки: научный факт — или миф?
Сегодня гипотеза о «шести рукопожатиях» широко распространена. Она популяризируется в художественных фильмах, телешоу и других явлениях массовой культуры, принцип «тесного мира» наглядно иллюстрируют социальные сети интернета, да и сама по себе идея доступности любого человека весьма притягательна. Кому не хочется быть «знакомым знакомого знакомого» английской королевы или Билла Гейтса, Джонни Деппа или Фиделя Кастро?.
.
Однако гипотезу зачастую трактуют неправильно: «я знаком с любым человеком на Земле через шесть рукопожатий» — так обычно говорят. Но «шесть» — это средняя длина цепочки, и до какого-нибудь африканского пигмея, тибетского монаха или полинезийского рыбака может оказаться все десять или пятнадцать «рукопожатий», если вообще удастся построить цепочку.
Второе распространенное заблуждение, связанное с «тесным миром», — что уже через один-два уровня знакомств мы имеем доступ к огромному числу людей. У каждого из нас, предположим, есть пресловутые сто друзей, у каждого из которых еще по сто друзей и т. д. На самом деле людям свойственно образовывать замкнутые группы: по месту проживания, по роду деятельности или по работе, по интересам и увлечениям, по политическим и религиозным воззрениям, по образовательному уровню и уровню доходов… а ведь где-то есть и кастовые системы с весьма жесткими границами. И если основательно взяться и посчитать, сколько всего у вас «знакомых знакомых», довольно скоро обнаружатся границы социальной группы (или нескольких групп), к которой вы принадлежите, и станет видно, что на третьем уровне вы имеете доступ не к миллиону человек, как казалось, а всего к нескольким тысячам или десяткам тысяч.
Кроме заблуждений, происходящих от неправильного понимания «теории шести рукопожатий», недостатки присущи и ей самой. Уже Фридеш Каринти в своем рассказе заметил, что человечество не всегда было целостным. Если Юлию Цезарю, писал Каринти, пришла бы в голову мысль связаться с одним из жрецов ацтеков или майя, жившим в Америке в одно время с ним, то у него ничего бы не вышло, невозможно было бы построить между ними цепочку ни из пяти, ни даже из трехсот звеньев — во времена Цезаря Америка была неизвестна европейцам.
И сейчас, в XXI веке, мир далеко не так монолитен и пронизан связями, как можно было бы предположить. По-прежнему существуют замкнутые или практически полностью изолированные от остального мира группы. Интернет, который, казалось бы, сокращает связи между людьми, на самом деле в разных частях мира доступен очень неравномерно. Следовательно, результаты экспериментов, эти «шесть рукопожатий», могут быть применимы к Европе, к США, к европейской части России, быть может, к отдельным крупным городам, но не ко всей территории Земли, в разных районах будут разные цифры.
С результатами описанных выше исследований тоже не все безупречно. В 2006 году Джудит Клейнфилд, профессор психологии из Аляскинского университета в Фэрбэнксе, обратила внимание, что 95% писем, отправленных входе эксперимента Милгрэма, не дошли до конечного адресата — то есть просто потерялись где-то на полпути. Она обратилась к результатам других подобных исследований и обнаружила там то же самое. Так, например, во время эксперимента Уоттса и Строгатца из 24000 писем дошли 384. «Если 95−97 писем из ста не доходят, можно ли говорить о доказательности такого эксперимента?- спрашивает Клейнфилд. — Почему мы в это верим? Соблазнительная идея, будто мы живем в ‘тесном мире’, где все знакомы со всеми максимум через шесть промежуточных знакомых, — это академический эквивалент городского мифа».
Исследование Microsoft, на первый взгляд подкупающее своими огромными числами (большие числа якобы не врут), тоже имеет свои недостатки: MSN-мессенджером пользуются 4% населения Земли, и эти 4% очень неравномерно распределены по планете — большая часть их приходится на США.
В России, например, сервису MSN раньше массово предпочитали ICQ. Итак, мы опять пришли к тому, что результат исследования корректен для ограниченной территории, для ограниченных групп людей, но не для человечества в целом.
Что такое «теория шести рукопожатий» — факт или миф, точно сказать нельзя. Истина, скорее всего, где-то посередине. Но, так или иначе, «теория шести рукопожатий» — это интересное предположение, и вероятно, что по мере движения в будущее, с увеличением плотности населения Земли, с распространением интернет-технологий и взаимопроникновением культур люди будут становиться ближе друг к другу.
Откуда пошло название «шесть рубежей отдаления»
Драматург Джон Гуэйр, автор пьесы «Шесть рубежей отдаления», с легкой руки которого гипотеза пошла в массы, говорит, что использовать в названии пьесы число «шесть» его подтолкнули исследования отнюдь не Милгрэма, а… Гульельмо Маркони, одного из изобретателей радио. В своей нобелевской речи Маркони сказал, что ему удалось передать читаемое сообщение на расстояние 2500 км.
Он подсчитал, что если строить передающие станции с таким радиусом передачи, то для покрытия всей населенной территории Земли потребуется всего шесть (точнее — 5,83) передатчиков. Гуэйр использовал это «шесть» как символ чего-то, охватывающего весь мир.
Игры «тесного мира»
Среди любителей кино известна игра «Шесть шагов до Кевина Бэйкона»: нужно найти цепочку до Кевина Бэйкона от любого другого актера (причем не обязательно современного, можно брать всю историю кинематографа). Цепочка строится по принципу «они снимались вместе» и не должна быть длиннее шести звеньев. Интересно, что повод для возникновения этой игры дал сам Бэйкон, в одном из интервью хвастливо заметивший, что те, с кем он снимался, в свою очередь снимались со всеми голливудскими актерами. Другая похожая игра распространена среди математиков, она называется «Число Эрдеша». Собственно число Эрдеша — это количество звеньев в цепочке совместных работ от заданного ученого до венгерского математика Пола Эрдеша, известного огромным количеством соавторских публикаций.
[источники]
источники
http://www.popmech.ru/technologies/11630-shest-rukopozhatiy-do-korolevy-elizavety-5-druzey-do-prezidenta/#full
http://secrets-world.com/interesting/10878-verna-li-teoriya-shesti-rukopozhatiy.html
http://www.therunet.com/articles/871-mir-tesen-teoriya-6-rukopozhatiy-v-epohu-sotssetey
Вот еще некоторые интересные теории: вот например Теория струн одной картинкой, а вот интересно Теория Дарвина — миф или реальность? Вот еще знаменитая Теория заговоров: От Медичи к Ротшильдам ну и конечно же Шесть альтернатив теории Большого взрыва
Tags: Интересно
Telegram channel
У всех шесть степеней разницы, а ты до сих пор не общаешься с Бейонсе
Шесть степеней разделения миф или мотивация?
Теоретически существует всего шесть степеней разделения между вами и всеми остальными в мире. Вы в одном градусе от всех, кого вы знаете, в двух степенях от всех, кого они знают, и так далее.
Теория шести степеней разделения, или шести рукопожатий, была впервые предложена венгерским писателем и драматургом Фридьесом Каринти в 1929. Его исследовал социолог Стэнли Милграм, опубликовавший свои выводы под названием «Проблема маленького мира» в майском номере журнала Psychology Today за 1967 год. Затем эта теория была популяризирована в пьесе 1990 года, написанной Джоном Гуаре, по которой был снят фильм с Уиллом Смитом в главной роли.
Это также стало частью игры, разработанной студентами колледжа в 1990-х годах, которая пытается связать актера Кевина Бэкона с киноиндустрией после того, как актер сказал во время интервью журналу Premiere, что «он работал со всеми в Голливуде или кем-то, кто работал с ними».
Семь миллиардов разлук
Сейчас в мире более семи миллиардов человек, и трудно поверить, что мы связаны с каждым другим человеком на планете. Действительно, многие люди отвергли теорию Фригьеса Каринти. Но в 2008 году Microsoft обнаружила, что расстояние между любыми двумя незнакомцами составляет в среднем ровно 6,6 градуса.
Возможно, это не идеально, но это показывает, что вы можете общаться с кем угодно в мире, если хотите. Друг друга друга друга друга знает Бейонсе, принца Гарри или Джастина Трюдо. Подумайте о силе, которая дает вам.
Сила (и паника) сети
Тем не менее, работа в сети кажется многим людям невыполнимой задачей. Люди часто жалуются, что никого не знают, но на самом деле мир тесен, особенно если вы ирландец. Каждый день в городах по всему миру люди со смутно знакомым акцентом сталкиваются друг с другом, а затем сразу же начинают искать общие связи друг с другом. Такое ощущение, что это нормально. Это практически встроено в нашу природу как ирландцев, но многие, хотя они могут вести такие разговоры, даже не задумываясь об этом в личных ситуациях, кажется, замирают, когда дело доходит до определения этой точки соприкосновения с профессиональными отношениями.
Теперь, как никогда ранее, люди доступны. Большинство политиков, бизнесменов, кинозвезд (даже Кевин Бейкон — у него более 650 000 подписчиков в Твиттере) сидят в социальных сетях. И у каждого есть адрес электронной почты. И все же вы не пытались написать Бейонсе по электронной почте, чтобы она использовала ваш продукт, или делового человека, которого вы хотите видеть в качестве наставника, или человека, которым вы больше всего восхищаетесь в своей отрасли. Вы можете добраться до всех из них. Вам просто нужно найти шесть правильных соединений, но вы никогда не сделаете это, если не попробуете.
Подробнее:
Подробнее: Как общаться, если вы застенчивы
Подробнее: Как узнать о декретном отпуске перед приемом на работу
Рукопожатия
Возраст от 11 до 14 лет
Уровень вызова
полезная связь с другой проблемой, опубликованной в этом
месяц:
Это похоже на определение количества строк в Mystic Rose.
Допустим, есть n человек. Первый человек пожимает руку
другие n-1 человек.
Затем второй человек пожимает руку другому n-2
люди.
И так далее, пока (n-1)-й человек не пожмет руку n-му
человек.
Итак, количество рукопожатий равно (n-1) + (n-2)… + 3 + 2 + 1, что равно (n-1)(n)/2.
Другой способ рассмотрения состоит в том, что каждый человек имеет в общей сложности n-1 рукопожатий, и есть n человек, поэтому будет (n-1)(n) рукопожатия, но это включает каждое рукопожатие дважды (1 и 2, 2 и 1) поэтому деление на 2 дает правильный ответ.
Асваат из Garden International Школа в Куала-Лумпуре, Малайзия, упомянула, что метод решение этой проблемы, связанной с метод, которым пользовался Гаусс, когда он был еще молодой студент.
Джо из начальной школы Хоув Парк также заметил связи с другой работой:
Если встретились, например, 10 математиков, то первый сделает 9
рукопожатий, второй делает 8, третий делает 7 и так далее, пока
десятый находит, что он уже со всеми поздоровался и так
больше не делает.
Это дает 9+8+7+6+5+4+3+2+1+0 рукопожатий, а это 45.
Но посмотрите на последовательность… это 9-й треугольник
число.
(см. рисунок
Triangle Numbers и/или Clever Carl)
Формула для T-го треугольного числа: T(T+1)/2
При задаче о рукопожатии, если есть n человек, то число
рукопожатий эквивалентно (n-1)-му треугольному числу.
Подставляя T = n-1 в формулу для треугольных чисел, мы можем вывести формулу для количества рукопожатий между n человек:
Количество рукопожатий = (n-1)(n)/2
Джейми из Garden International Школа согласилась и использовала это понимание, чтобы исправить ошибку Сэма. рассуждение:
Метод Сэма неверен, потому что он не разделил ответ на 2. Если вы не разделите его на 2, вы будете считать количество рукопожатия между парами математиков дважды.
Если встречаются 20 математиков:
20 x 19 = 380
380 / 2 = 190 (общее количество рукопожатий)
Если встречается 161 математик:
161 x 160 = 25760
25760 / 2 = 12880 (общее количество рукопожатий)
Может ли быть ровно 4851 рукопожатие на собрании, где все пожимают друг другу руки?
Мы знаем, что 4851 рукопожатие приходится на 20 математиков и 160
математики.
Общее количество рукопожатий = 100 x 99 / 2 = 4950
Это слишком много, так что теперь я попробую 99 математиков.
Общее количество рукопожатий = 99 x 98 / 2 = 4851
Следовательно, может быть ровно 4851 рукопожатие, когда 99
встречаются математики.
Может ли быть ровно 6214 рукопожатий на собрании, где все пожимают друг другу руки?
Начнем с проверки 112 математиков.
Общее количество рукопожатий = 112 x 111/ 2 = 6216
Это слишком много, так что теперь я попробую 111 математиков.
Общее количество рукопожатий = 111 x 110 / 2 = 6105
Это слишком мало, поэтому не может быть ровно 6214 рукопожатий.
Джозеф из Bradon Forest School и Табита из школы Норвуд использовала аналогичные рассуждения: 92 -99 = 97024$
Так что да, если 99$ математиков встретятся, то будет 4851$ рукопожатия
$6214$ рукопожатия?
Нет, ближайшее треугольное число $6216$, а $6214$ не является
число треугольника
$3655$ рукопожатия?
Да, $86$ Математики
$7626$ рукопожатий?
Да, $124$ Математики
$8656$ рукопожатий?
Нет, ближайшее треугольное число $8646$, а $8656$ не является
номер треугольника.