Закон шести рукопожатий: «ВКонтакте» запустила приложение для проверки теории шести рукопожатий

теория шести рукопожатий верна, но мы ещё ближе друг к другу

«Теория шести рукопожатий»

«Теория шести рукопожатий» гласит, что между двумя людьми на планете существует не больше, чем пять-шесть уровней связей. Изначально теория началась с социологии, но в скором времени распространилась и на другие научные области. С приходом интернета в жизнь человека закон шести рукопожатий все чаще подтверждается на практике.

Содержание

1. Что такое «теория шести рукопожатий»
2. Появление «теории шести рукопожатий»
3. «Число Эрдеша»
4. Самое масштабное исследование теории
5. Эксперименты в социальных сетях
6. Как можно легко понять, работает ли теория, на примере соцсети ВКонтакте

Что такое «теория шести рукопожатий»

Суть закона заключается в том, что каждый человек в мире знаком с любым другим человеком через ряд общих друзей или знакомых. Обычно такая цепочка состоит из пятерых-шестерых людей. Это означает, что вы с большой вероятностью можете быть знакомы даже с вашим кумиром через кратчайшую цепочку, состоящую из звена в пять-шесть человек.

Появление «теории шести рукопожатий»

Первыми гипотезу шести рукопожатий предложили ученые-психологи из США — Стэнли Милгрэм и Джеффри Трэверс. Исследователи провели эксперимент в двух городах США. Стэнли Милгрэм раздал по одному конверту тремстам людям, они должны были передать письмо через своих друзей, родственников или знакомых в соседний город. До места назначения дошло шестьдесят конвертов. Ученый сделал подсчеты и обнаружил, что каждое из писем прошло через руки пятерых людей. Этот эксперимент получил название «Мир тесен» и не на шутку взволновал общественность.

«Число Эрдеша»

Благодаря математику из Венгрии Палу Эрдешу теория была успешно подтверждена практикой. Математик написал за свою жизнь 1525 научных работ совместно с другими авторами. Математические подсчеты показали, что цепочка из авторов, когда-либо сотрудничавших с Эрдешем, состояла из пяти человек. Отсюда возникло такое понятие как «число Эрдеша», с помощью которого определяется кратчайшая цепочка соавторства по совместным научным статьям от определенного ученого до самого Пала Эрдеша.

Самое масштабное исследование теории

Но самое значимое исследование, подтверждающее «теорию шести рукопожатий», стал эксперимент Юрия Лесковца и Эрика Хорвитца — сотрудников компании Microsoft. В 2006 году Лесковец и Хорвитц проанализировали 30 миллиардов сообщений от 240 миллионов людей в течение тридцати дней. Пользователи общались в мессенджере MSN. На обработку и анализ данных у экспертов ушло два года. Юрий и Эрик брали во внимание пол, возраст, геолокацию и контакты пользователей MSN. После подсчета данных оказалось, что участников эксперимента разделяет друг от друга шесть связей.

Эксперименты в социальных сетях

Социальные сети прочно вошли в жизнь современного человека. Благодаря прелестям всемирной паутины сегодня можно легко отследить цепочку общих знакомых. Если к нам на страницу в Фейсбуке или в ВКонтакте добавляется новый друг, мы часто замечаем, что у нас существуют общие друзья. Фейсбук тоже решил провести исследование теории шести рукопожатий, но результаты соцсети отличались от результатов остальных экспериментов. Эксперты из Фейсбука обнаружили, что цепочка состоит из 4,4 звена. Но различия в результатах можно объяснить тем, что этой социальной сетью пользуется далеко не 100% пользователей.

Как можно легко понять, работает ли теория, на примере соцсети ВКонтакте

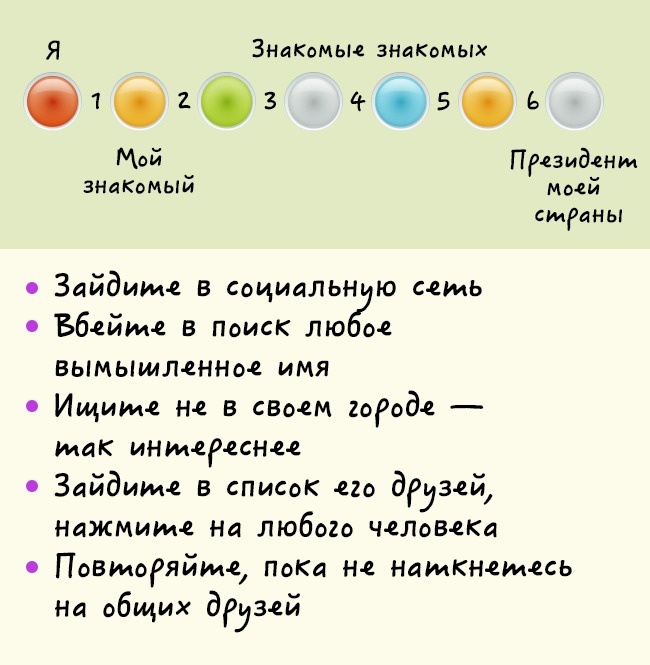
Вы можете и сами провести интересный эксперимент.

Возьмем для примера соцсеть ВКонтакте:

1. Выберите в поисковике любого незнакомого человека с любым именем и фамилией, лучше из другой местности;
2. Зайдите к нему на страницу и откройте список друзей. Выберете самого первого друга;
3. Зайдите к нему на страницу и выберете первого друга этого человека;
4. Повторяйте действие минимум 5 раз. Вероятнее всего, на этом этапе вы обнаружите своих знакомых.

Правила шести рукопожатий, или поиск в ширину | by Vincent

Сегодня мы поговорим о «правиле шести рукопожатий». Не совсем, а вроде.

Правило 6 рукопожатий, также известное как 6 степеней разделения, заключается в том, что все люди в мире находятся на расстоянии 6 или меньше соединений друг от друга.

Эта интересная концепция станет нашей основой для изучения темы, более связанной с информатикой: алгоритмов поиска пути.

Вот что мы рассмотрим:

• Что такое алгоритмы поиска пути
• Что такое граф
• Различные типы графов
• Поиск в глубину и поиск в ширину
• Как работает BFS
• Тестирование BFS с помощью правила 6 рукопожатий
  2 , алгоритмы поиска пути — это алгоритмы, которые помогают нам найти путь между двумя точками.

  Поиск в глубину , Поиск в ширину и Алгоритм Дейкстры — это разные алгоритмы, которые помогают нам решать задачи, требующие обхода графов.

  Алгоритмы этих типов можно использовать по-разному: собирать кубик Рубика за наименьшее количество ходов, вычислять кратчайший путь от работы до дома или даже определять уровень ваших отношений с незнакомцем в LinkedIn.

  Сегодня мы более подробно рассмотрим алгоритм поиска в ширину, чем он отличается от алгоритма поиска в глубину и как его реализовать.

  Чтобы лучше понять, как работают эти алгоритмы, давайте сначала определим, что такое графы.

  Граф — это набор соединений. Он состоит из узлов и ребер. Если бы у нас был граф, представляющий совокупность людей, каждый человек был бы узлом, а каждое отношение было бы ребром, соединяющим два узла.

  Мари дружит с Джозефом. Джозеф дружит с Домом. У Мари вторая степень связи с Домом.

  Графики бывают разных видов и видов. Ориентированные и неориентированные графы, взвешенные и невзвешенные графы — это способы их классификации.

  Направленный против ненаправленного

  Примером ориентированного графа может быть группа сталкеров (тьфу). Винсент следит за Бобом на Facebook. Боб его не знает. Но он преследует Мари. В таком графе человек знает другого, но это не взаимно. Это односторонние отношения. Таким образом, края будут направлены.

  Пример неориентированного графа больше похож на реальность, где, если Винсент знает Боба, скорее всего, Боб знает Винсента.

  Взвешенный и невзвешенный

  У нас также есть взвешенные и невзвешенные графики.

  Невзвешенный граф — это граф, в котором ребра имеют одинаковое значение и одинаковый вес. Представьте, что вы хотите поехать в центр города и смотрите на разные автобусные маршруты. Это дождливый день, вас не волнует продолжительность поездки, вы хотите, чтобы у вас было как можно меньше пересадок, чтобы вы не ждали под дождем. Вы ищете самую простую поездку. Автобусные остановки будут узлами, а автобусные рейсы — ребрами.

  • Для поездки А потребуются 2 автобуса и 1 линия метро.
  • Для поездки B потребуется 1 автобус.

  В этом примере нам все равно, будет ли поездка быстрее. Нам просто нужен тот, у которого наименьшее количество шагов.

  Взвешенный граф противоположен. Ребра имеют разные значения. Следовательно, кратчайший путь — это не обязательно путь с наименьшим количеством шагов. Возьмем тот же пример. Вы едете на автобусе в центр города, но на этот раз опаздываете на свой первый рабочий день. Вам нужен самый быстрый маршрут, независимо от того, сколько автобусов вам нужно. Опять же, каждая автобусная остановка/станция метро является узлом. Длина поездок — это ребра. Чем дольше поездка, тем выше вес.

  • Для поездки A потребуется 2 автобуса (10 и 5 минут) и 1 линия метро (10 минут)
  • Для поездки B потребуется 1 автобус (30 минут)

  каждый автобус, а не только количество занятых автобусов. Мы придаем значения краям.

  Теперь, когда мы разобрались с графиками, давайте взглянем на поиск в ширину и поиск в глубину. Оба они являются алгоритмами поиска по невзвешенным графам.

  Чтобы найти кратчайший путь во взвешенном графе, вам может понадобиться изучить алгоритм Дейкстры (сегодня мы не будем его рассматривать).

  Этот алгоритм выполняет поиск по деревьям и графам, исследуя, насколько это возможно, каждую ветвь дерева/графа.

  На следующем изображении показано, как алгоритм будет исследовать дерево.

  Начиная с корня, он будет исследовать первый дочерний элемент слева (B), затем снова самый левый дочерний элемент (E), пока не попадет в тупик. Затем он поднимется на уровень выше и посетит самый левый дочерний узел, который еще не был посещен (F), и продолжит повторяться.

  Этот алгоритм использует стек для отслеживания всего. Если кратко схематизировать, то это будет выглядеть следующим образом.

  А попадает в стек. B помещается поверх A. E помещается поверх B. E удаляется из стека. F помещается поверх B. F удаляется. Б удаляется. C ставится поверх A. И так продолжается и продолжается, вы поняли идею.

  Как видите, это структура типа LIFO, Last In First Out.

  Кольцевая колонна штабелирования также является конструкцией LIFO.

  Это хороший алгоритм, но если бы мы искали узел D, мы бы сделали много дополнительных вычислений для узла, который находится прямо под нашим корневым узлом. У нас также могут быть некоторые проблемы, если бы наш график имел другую форму, например, возьмем это изображение:

  *На этом графике алгоритм начинается с самого правого узла, но применяется та же концепция.

  Если бы мы искали узел F, мы бы обнаружили, что он исходит из узла G, и тогда алгоритм остановился бы. Давая нам путь из 6 ребер.

  Однако это не самый короткий путь. Путь A-I-C-F дал бы нам только 3 ребра, будучи кратчайшим путем.

  Здесь в игру вступает поиск в ширину.

  Как и DFS (поиск в глубину), поиск в ширину — это алгоритм поиска пути для обхода или поиска пути в невзвешенных структурах данных дерева или графа.

  В отличие от DFS, вместо более вертикального (глубокого) поиска, BFS исследует слой за слоем, более горизонтально.

  Он просматривает первый слой узлов, которые являются соседями корневого узла, и если они не являются теми, которые он ищет, он помещает соседей этих узлов в очередь и продолжает работу.

  В отличие от своего аналога, BFS использует очередь, а не стек. Тип структуры FIFO, First In First Out. Это будет выглядеть следующим образом:

  А ставится в очередь. B, C, D становятся в очередь. A удаляется из очереди. E и F идут в очередь. B удаляется из очереди. G становится в очередь… и так далее, и тому подобное.

  Структура типа «первым прибыл – первым обслужен».

  Проблема: Мы хотим найти путь от узла А к узлу Z

  1. Поместите узел А в очередь.
  2. Найдите 1-й узел в очереди. Если это то, что вы ищете, вы сделали! Если не продолжить…
  3. Поместить всех соседей узла в очередь.
  4. Пометить узел как найденный
  5. Удалить узел из очереди
  6. Повторять шаги 2–5 до тех пор, пока а) вы не нашли узел Z или б) пока очередь не пуста.
  7. Если ваша очередь оказывается пустой, путь от узла A к узлу Z не существует.

  Чтобы лучше понять BFS, мы напишем собственный алгоритм BFS, основанный на правиле 6 рукопожатий. Не совсем, но вроде. Для простоты у нас будет мир из 9 человек.

  1. Начнем с создания набора данных, представляющего наш мир. Вот массив объектов. Каждый объект — это человек с именем и множеством друзей.

  2. Нам нужно смоделировать нашу задачу в виде графа. Мы знаем, что граф состоит из узлов, поэтому давайте создадим класс Node.

  Чтобы построить наш класс, мы должны знать, что нам нужно в нашем алгоритме.

  • Нам нужен человек, которого мы ищем. => name
  • Нам нужны соседи, с которыми он связан. => друзья
  • Нам нужен метод, позволяющий легко добавлять друзей. => addFriend()
  • Нам нужен способ узнать, был ли узел уже проверен. => проверено логическое значение
  • Нам нужен метод, чтобы пометить узел как проверенный => isChecked()
  • Мы также хотим знать, какой путь ведет к этому узлу, поэтому, когда мы найдем нашу цель, мы можем изменить путь и узнать все связи, которые мы сделали на этом пути. => путь
  • Нам нужен метод для создания этого пути => pushBy()

  3. Далее нам нужно преобразовать наш набор данных в граф

  Мы проходим через наш набор данных и создаем узлы из всех объектов. Затем мы помещаем эти узлы в нашу константу myGraph.

  4. Теперь самое сложное: нам нужно создать алгоритм, который будет проходить через наш граф.

  Сначала мы хотели бы иметь дело с именами, а не с узлами. Итак, давайте создадим небольшую вспомогательную функцию, которая делает именно это.

  Отлично!

  Теперь, выполнив 7 шагов, которые мы описали ранее, давайте создадим окончательную функцию.

  Ну вот. Мы преобразовали наш набор данных в график, а затем использовали алгоритм поиска в ширину, чтобы найти кратчайший путь между двумя людьми.

  Чтобы получить доступ к более удобной для копирования/вставки версии этого кода, в нижней части статьи приведена суть.

  Если вы хотите узнать больше об алгоритмах, я бы порекомендовал новичкам книгу «Алгоритмы грокинга» Адитьи Й. Бхаргавы. Это книга для начинающих, в которой можно освоить такие алгоритмы, как поиск в ширину, алгоритм Дейкстры и K-ближайших соседей.

  Grokking Algorithms

  Grokking Algorithms — это полностью иллюстрированное, понятное руководство, которое научит вас применять распространенные алгоритмы к…

  www.manning.com

  Правило шести рукопожатий — De Economytrist

  В 1994 году четверо студентов колледжа Олбрайт создали игру под названием «Шесть степеней Кевина Бэкона». Цель этой игры — связать любого актера голливудской сцены с актером Кевином Бэконом, используя не более 5 актеров, с которыми они работали (в) напрямую. Идея пришла в голову студентам после того, как Кевин Бэкон заявил в интервью журналу Premiere, что «он работал со всеми в Голливуде или с кем-то, кто работал с ними».

  После того, как юные студенты и Бэкон были приглашены на телешоу, чтобы объяснить свою игру, его популярность значительно возросла. Была выпущена даже настольная игра, основанная на концепции, и изобретено «число Бэкона». Это число — степени разделения между актером и Кевином Бэконом. Эта новая игра означала большой успех Кевина Бэкона, хотя сама концепция игры не была новой.

  Шесть степеней разделения — это идея о том, что все люди связаны друг с другом не более чем шестью социальными связями. Эта концепция часто упоминается как «Правило шести рукопожатий» и первоначально была сформулирована Фригьесом Каринти в 1929. Теории, основанные на этой идее, уже обсуждались после Первой мировой войны, но именно Каринти опубликовала серию рассказов, в том числе статью под названием «Звенья цепи». В этой истории он, в частности, говорит, что, по его мнению, современный мир «сжимается» из-за постоянно растущей взаимосвязанности людей. В результате этой гипотезы персонажи сказки полагали, что любые два человека могут быть связаны не более чем пятью знакомыми.

  Идея Каринти о шести степенях разделения вызвала большой интерес, конечно же, у психологов и в культурных проектах. Американский драматург Джон Гуар написал пьесу в 1990 и выпустил в 1993 году фильм, популяризировавший его. В пьесе уместно размышляет об идее, что любые два человека связаны не более чем пятью другими.

  Игре Кевина Бэкона предшествовала игра Джона Л. Салливана, в которой люди просили других «пожать руку, которая пожала руку, которая пожала руку, которая пожала руку «великому Джону Л.»

  Более того, эта концепция удивительно часто использовалась в различных формах развлечений. Несколько песен и более десяти телешоу были основаны на шести степенях разделения. Одним из таких шоу была еженедельная секция 9.0201 Досье Костерс на производство Man Bijt Hond , в котором всемирное событие прошлой недели будет связано с Густавом Костерсом, обычным гражданином Фландрии, в шесть шагов.

  Различные фильмы также были основаны на этой концепции, например, оскароносный фильм Вавилон . В этом фильме жизни всех героев были тесно переплетены, хотя они и не знали друг друга и жили за тысячи километров друг от друга.

   

  Очевидно, можно сделать вывод, что феномен «маленького мира» пробился через развлечения, но доказана ли эта теория? Для проверки концепции было проведено несколько исследований.

  Одним из таких исследований является эксперимент Милгрэма «Маленький мир», в ходе которого степень проверялась среди населения США. В 1973 году Милгрэм использовал моделирование на довольно ограниченном количестве компьютеров и предсказал, что между гражданами США существует примерно три степени разделения. Однако его эксперимент был масштабным, что, безусловно, отличается от его тестирования в глобальном масштабе. Он также не включает изолированные группы людей, такие как коренное население Бразилии. Эти группы не могли иметь никаких контактов с остальным миром. Поэтому заявление о «шести степенях» часто называют «академическим городским мифом».

  К счастью, развитие социальных сетей в последние десятилетия и, следовательно, возможность подключения к сети, возможно, могут служить доказательством существования этого феномена. Как для Facebook, так и для Twitter исследователи дали многообещающие результаты. В 2011 году группа данных Facebook опубликовала две статьи, в которых говорилось, что среди всех пользователей Facebook на момент исследования среднее расстояние составляло 4,74.

  Вероятностные алгоритмы применялись к статистическим метаданным для проверки точности измерений. Также было установлено, что 99,91% пользователей Facebook были взаимосвязаны, образуя большой связанный компонент. Для сравнения, компания Sysomos, занимающаяся мониторингом социальных сетей, заявила, что пользователи Twitter связаны примерно на расстоянии 4,67.

  Кроме того, LinkedIn фактически частично основан на этой концепции, поскольку сеть состоит из связей первой, второй и третьей степени и других членов групп LinkedIn. Кроме того, LinkedIn уведомляет пользователя о том, сколько общих связей у него и любого другого пользователя

   

  Математики также пытались подойти к этой идее математически: людей, которых мы хотим соединить, можно рассматривать как узлы, а их связи — как ребра. Тогда, согласно шести степеням разделения, максимальная длина пути между двумя узлами должна быть равна шести.

  В более простом случае для числа Бэкона можно использовать алгоритм кратчайшего пути, так как набор узлов ограничен количеством актеров в Голливуде. Эта сеть по-прежнему будет чрезвычайно большой, но гораздо более управляемой, чем сеть, включающая все население мира.

  Чтобы доказать полную концепцию, нужно построить произвольное доказательство для каждой пары узлов. Уоттс и Строгац показали, что средняя длина пути между двумя узлами в случайной сети равна

  степеней разделения = ln N / ln K,

  , где N равно общему количеству узлов1 и . K — количество знакомств на узел. Таким образом, если N = 7 000 000 000 и

  K = 45, то Степеней разделения = 22,67/3,81 = 5,96.

  Математическое решение дает довольно надежный результат. Однако между использованием математики и реальным миром все же есть некоторые важные различия. Например, нельзя просто считать, что у среднестатистического человека 45 знакомых и, как было сказано ранее, не учитываются группы населения, отделенные от остального мира.

  Доказано это или нет, но концепция шести степеней свободы популярна в различных областях и наверняка будет исследована в будущем.

  No related posts.