Ученые создали самую точную 2D-карту мира
18 февраля 2021
Реальный мир космосаиещё 3
У всех нас есть свои любимые мировые карты, в центре которой находится континент, который мы называем своим домом. И когда эта карта мира переворачивается или смещается влево или вправо, все кажется… неуравновешенным.
Фото: Реальный мир космосаРеальный мир космоса
Это отражение того, как карты могут влиять на то, как мы видим и понимаем мир.
Видео дня
Теперь группа исследователей переосмыслила подход и создала двустороннюю карту — круглую, похожую на Землю, но также плоскую, как блин, — в попытке дать нам менее искаженное представление о мире.
«Мы предлагаем кардинально другой вид карты», — сказал астрофизик Принстонского университета Дж. Ричард Готт, который разработал новый разворот вместе с математиком Робертом Вандербреем и физиком Дэвидом Голдбергом из Университета Дрекселя в Филадельфии.
Трио намеревалось создать плоскую карту с наименьшими возможными ошибками после создания системы для оценки существующих карт по тому, насколько они однобокие или перекос, и сколько областей и расстояний на картах были изогнутыми.
«Мы считаем, что это самая точная плоская карта Земли», — написали исследователи, когда опубликовали свои методы на предпечатном сайте arXiv.org перед рецензированием. Вы можете ознакомиться с результатами:
«Любая плоская карта сферы не может быть идеальной, но наша карта намного лучше, чем предыдущие, в минимизации ошибок в локальных формах, областях, изгибах, расстояниях и граничных разрезах», — сказал Готт.
Математически невозможно представить поверхность сферы в виде плоской карты без каких-либо искажений, поэтому создателям карт приходится прибегать к некоторым математическим уловкам, чтобы достоверно представить одни земные особенности, жертвуя другими.
Некоторые карты мира предназначены для сохранения формы стран (так называемые конформно-конические проекции Ламберта), в то время как другие карты — глобусы, выпуклые на экваторе — сохраняют площадь.
Наложение сотен карт за раз показывает, насколько искажается мир, когда картографы пытаются его сплющить, как показывает в этой интерактивной визуализации специалист по данным Майкл Фриман из Информационной школы Вашингтонского университета:
Судя по имеющимся у нас картам, лучший универсал — это компромисс.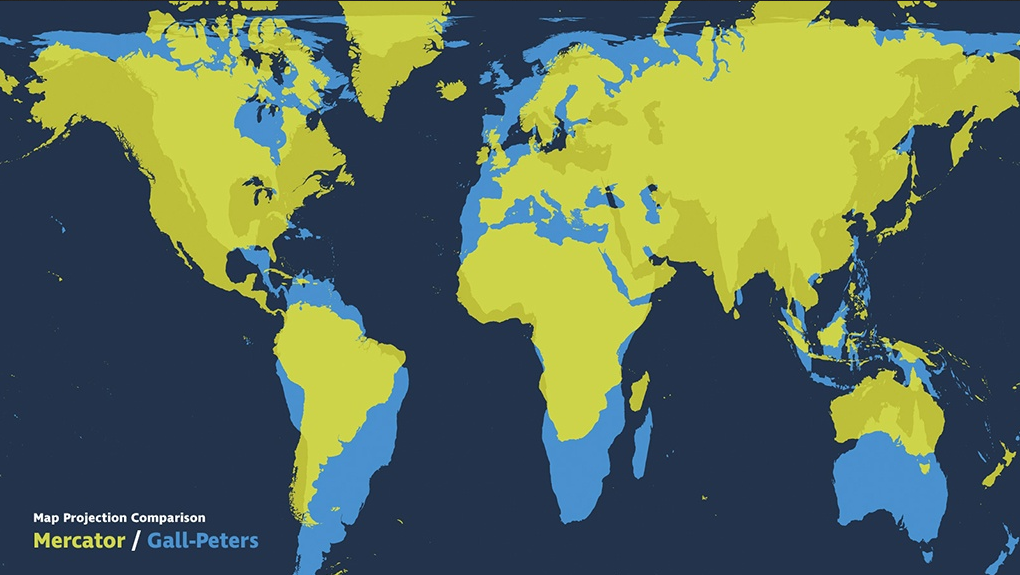 Известная как проекция Винкеля Трипеля и используемая National Geographic для создания карт мира, она сводит к минимуму искажения по площади, направлению и расстоянию.
Известная как проекция Винкеля Трипеля и используемая National Geographic для создания карт мира, она сводит к минимуму искажения по площади, направлению и расстоянию.
Северное и Южное полушария могут быть размещены по обе стороны от экватора по краю, как вы можете видеть ниже.
Gott, Vanderbei & Goldberg
По словам исследователей, что расстояния между океанами и полюсами точны и легко измеримы, поэтому это может быть полезным инструментом для обучения детей окружающему миру.
Даже с учетом улучшений, в этой карте диска все еще есть некоторые искажения, но не такие большие, как в других проекциях. Области по краям в 1,57 раза больше, чем в центре.
Но, по крайней мере, эта карта придает новый смысл термину «плоская Земля».
Наука и техника,Дэвид Голдберг,Принстонский университет,National Geographic,
1Создана самая точная «плоская карта» Земли
Земля — это сфера, поэтому как ее точно изобразить на двухмерной карте? Новое исследование показало, что просто расплющите Землю в два блина, один из которых изображает северное полушарие, а другой — южное, с экватором, проходящим по краю.
Читай также: Составлена самая точная карта Земли
По словам исследователей, эти два «блина» представляют собой наиболее точную плоскую карту Земли из когда-либо созданных. В отличие от других плоских карт, новая круговая карта не уменьшает и не увеличивает площадь определенных океанов или суши — например, на многих двухмерных картах Гренландия изображена примерно такого же размера, как Африка, хотя на самом деле Африка в 14 раз больше.
Кроме того, в отличие от некоторых прямоугольных карт, которые очень большие, «эту карту можно держать в руке», — сказал в своем заявлении ведущий исследователь Дж. Ричард Готт, почетный профессор астрофизики Принстонского университета. «Карту можно распечатать спереди и сзади на одной странице журнала, чтобы читатель мог вырезать ее».
Создание точных 2D-карт на протяжении веков преследовало картографов. Чтобы помочь определить различные проблемы, с которыми сталкиваются плоские карты, Готт и со-исследователь Дэвид Голдберг, профессор физики в Университете Дрекселя в Филадельфии, создали систему для оценки существующих плоских карт и опубликовали свои результаты в 2007 году в журнале Cartographica.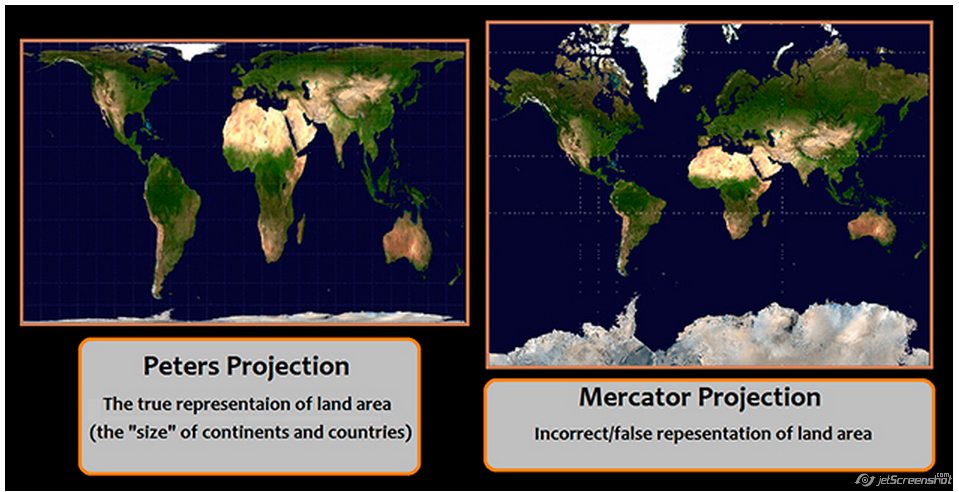 Их система оценивала 2D-карты по шести типам искажений: локальные формы, площади, расстояния, изгиб (изгиб или искажения кривизны), асимметрия (однобокость) и граничные разрезы (разрывы непрерывности, такие как разделение Тихого океана). По их словам, карты, получившие более низкие оценки, были более точными. Хорошо спроектированные глобусы, которые имеют сферическую форму, как Земля, не заработают ноль баллов.
Их система оценивала 2D-карты по шести типам искажений: локальные формы, площади, расстояния, изгиб (изгиб или искажения кривизны), асимметрия (однобокость) и граничные разрезы (разрывы непрерывности, такие как разделение Тихого океана). По их словам, карты, получившие более низкие оценки, были более точными. Хорошо спроектированные глобусы, которые имеют сферическую форму, как Земля, не заработают ноль баллов.
Читай также: Астрономы показали настоящую форму Земли
«Нельзя сделать все идеально на плоской карте Земли», — сказал Готт. «Карта, на которой хорошо получается одно, может не подходить для изображения других вещей». Возьмем, к примеру, карту мира, с которой знакомо большинство людей, — проекция Меркатора, основной продукт, используемый во многих классах, и основа для Google Maps. По словам исследователей, хотя проекция Меркатора хорошо отображает локальные формы, она искажает участки поверхности вблизи Северного и Южного полюсов, поэтому эти области часто обрезаются.
Создана самая точная «плоская карта» Земли / QAI Publishing
Читай также: На Земле нашли 657 новых островов
Согласно рейтинговой системе команды, самая популярная проекция плоской карты — это карта Винкеля Трипеля, созданная в 1921 году, когда ее предложил немецкий картограф Освальд Винкель, и которую сейчас использует Национальное географическое общество. Эта карта получила низкий балл — 4,563, но у нее все еще была проблема с «разрезанием границ», потому что она разделяла Тихий океан на две части, одна часть которых была справа, а другая — слева от карты. Этот раскол создает иллюзию, что Азия и Гавайи дальше друг от друга, чем они есть на самом деле.
Создана самая точная «плоская карта» Земли / Photitos2016
Читай также: Америку открыли китайцы? Найдена карта 1418 года
Чтобы обойти эту проблему разделения границ, исследователи подошли к созданию карт с новой точки зрения, надеясь разработать «плоскую карту с наименьшими возможными ошибками», — сказал Готт.
Конечный результат, карта блинов, заимствовал идеи из предыдущих исследований многогранников или многогранных трехмерных форм. В 1943 году американский архитектор Ричард Бакминстер Фуллер нарисовал контуры правильных форм, составляющих карту мира, и написал инструкции о том, как его карту можно сложить в многогранный глобус. Но хотя Фуллер хорошо детализировал континенты, он не был так точен с океанами, что привело к ошибкам. Например, Австралия и Антарктида были слишком далеки от реальности.
Создана самая точная «плоская карта» Земли / Thomas D. McAvoy
Карта блинов также имеет меньшие ошибки расстояния, чем любая другая плоская 2D-карта. Например, его конфигурация означает, что расстояния не могут быть больше или меньше 22,2% от реальных, сказал Готт. Для сравнения, проекции Меркатора и Винкеля Трипеля имеют чрезвычайно высокие ошибки расстояния около полюсов, а также у левого и правого краев карты.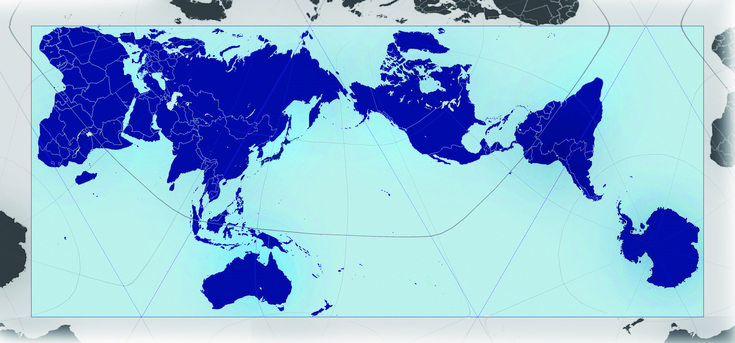
Напомним, ранее сообщалось, что в Сеть выложили интерактивную карту всех сражений в истории человечества.
Хотите знать важные и актуальные новости раньше всех? Подписывайтесь на Bigmir)net в Facebook и Telegram.
- Теги:
- карта
- карта Земли
6 основных типов картографических проекций мира
Карты существуют уже более 5000 лет. Древний процесс картографии заложил основы карт, искусства и науки. Карты могут быть разных форм. Политические карты показывают политические объекты, такие как штаты, границы стран, столицы и расположение городов. Политические карты предназначены для обозначения стран отдельными цветами для облегчения идентификации на земном шаре. Физические карты растительности — это тип карты, на которой показан рельеф местности вместе с типами растительности, которые занимают определенные регионы по всему миру. Физический глобус Replogle показывает естественные растительные особенности пустынь, тропиков, лугов, лесов, тундры и ледяных шапок.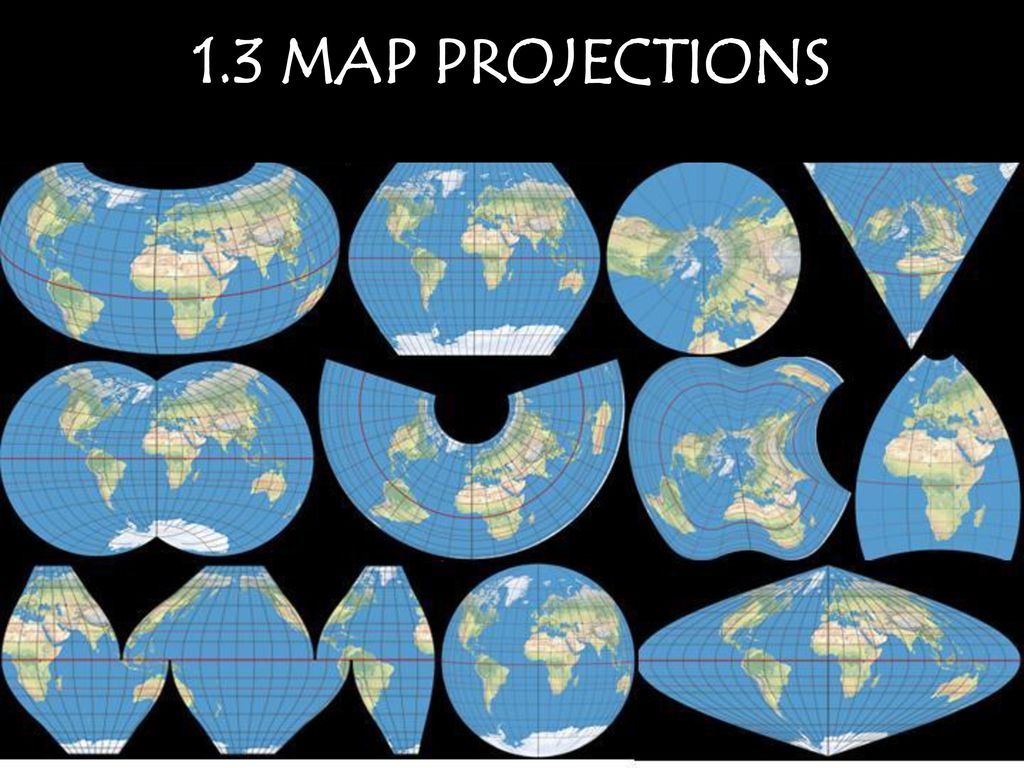
Основные типы картографических проекций
Меркатор — самая популярная конформная картографическая проекция. Картографическая проекция Меркатора была создана Герардом Меркатором в 1594 году. На ней меридианы изображались равноотстоящими линиями. Проекция используется для различных навигационных прокладок судовых маршрутов. Карты Меркатора считаются самыми простыми и легкими настенными картами для отображения местоположения и расстояний между линиями широты и долготы.
Робинсон
Картографическая проекция Робинсона была создана Артуром Х. Робинсоном в 1963. Одной из главных сильных сторон карты Робинсона является ее способность показывать точное представление о формах и местоположениях суши с минимальными искажениями в центре карты. Проекция Робинсона использует изогнутые линии для долготы и параллельные прямые линии для широты, как на настенной карте от Replogle.
Гомолосинус Гуда
Картографическая проекция Гуда была разработана Джоном Полом Гудом в 1925 году. Одной из основных ключевых особенностей гомолозиноидной проекции Гуда является ее способность минимизировать искажения для всего мира. Континенты, показанные на картах гомолосины Гуда, имеют правильные размеры пропорционально друг другу. Одним из основных недостатков этого типа проекции является использование расстояний, направлений и углов, которые не отображаются точно из-за искажений.
Трипель Винкеля
Проекция Винкеля Трипеля была разработана Освальдом Винкелем в 1921 году. Одно из основных применений этого типа проекции заключается в том, что он показывает континенты и страны с очень небольшими искажениями, в результате чего массивы суши отображаются очень точно. показаны на картах с очень хорошей детализацией.
Полярная проекция
Полярная проекция в основном используется для отображения северных или южных полярных регионов Арктики и Антарктиды. Полярная проекция является разновидностью азимутальной проекции. Этот тип проекции показывает истинные площади и формы стран и континентов с очень небольшим искажением.
Полярная проекция является разновидностью азимутальной проекции. Этот тип проекции показывает истинные площади и формы стран и континентов с очень небольшим искажением.
AuthaGraph
Проекция AuthaGraphy была создана японским архитектором Хадзиме Нарукавой в 1999 году. Она считается самой точной проекцией в мире картографии благодаря способу отображения относительных площадей суши и океанов с очень небольшим искажением формы. Одной из ключевых особенностей проекции AuthaGraph является способ отображения Земли без тупиков или конечных точек. Это приводит к очень уникальным видам карты под разными углами.
Вывод
Мы в Replogle Globe учитываем многие аспекты различных проекций при разработке наших глобусов и карт. Мы с большой осторожностью и точностью определяем наиболее точную проекцию карты мира для конкретного проекта, прежде чем двигаться дальше. Благодаря такому вниманию к деталям мы с гордостью представляем одни из самых точных и современных глобусов на рынке.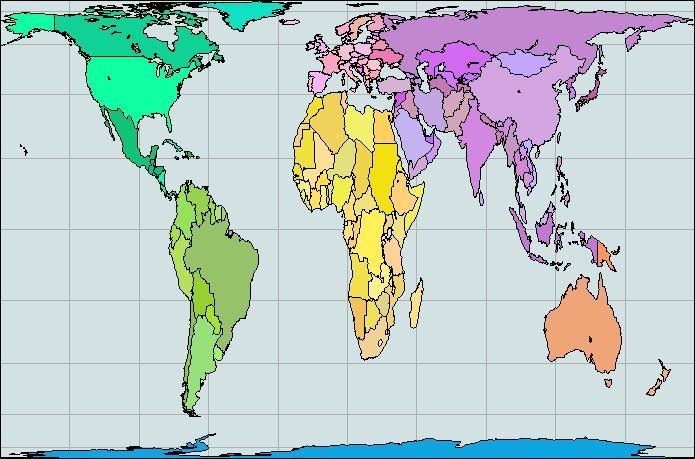 Свяжитесь с нами!
Свяжитесь с нами!
Автор: Рик Вайнгард
Картографические проекции
Сплющивание Земли
Невозможно сгладить Землю, не исказив ее каким-либо образом. Возьмем апельсиновую корку: если вы хотите положить ее ровно, вам придется растянуть ее, раздавить и разорвать. То же самое и с Землей: если мы хотим составить карту, нам нужно исказить поверхность Земли, чтобы сделать ее плоской. Хорошая новость заключается в том, что картографические проекции позволяют систематически искажать изображения; мы точно знаем, как вещи растягиваются или сжимаются в любой данный момент. У нас есть много разных картографических проекций, потому что каждая из них имеет разные модели искажения — существует более одного способа сгладить апельсиновую корку. Некоторые проекции могут даже сохранить определенные черты Земли, не искажая их, хотя и не могут сохранить все.
Свойства проекции
Мы часто говорим о картографических проекциях с точки зрения способов, которыми они искажают или сохраняют определенные свойства Земли, которые мы называем свойствами проекции . Существует четыре основных свойства:
Существует четыре основных свойства:
Площадь — некоторые проекции искажают площади (например, проекция Меркатора)
Обратите внимание, что размер Гренландии примерно равен Южной Америке в проекции Меркатора. На самом деле Южная Америка в восемь раз больше Гренландии. Проекция Меркатора неправильно сохраняет площадь, особенно по мере приближения к полюсам. С другой стороны, одним из видов проекции, которая не искажает площадь, является цилиндрическая равновеликая площадь.
Обратите внимание, что Гренландия выглядит правильно по сравнению с Южной Америкой. Проекции, которые сохраняют площади, называются эквивалентными или равновеликими проекциями. Картографическая проекция либо везде сохраняет площади, либо везде их искажает. Это свойство «все или ничего».
Форма — Некоторые проекции искажают «форму» объектов (например, Азимутальная Эквидистанта)
На проекции выше посмотрите, как Австралия справа неузнаваема, а Новая Зеландия вытянута кольцом вокруг левой край карты. Эта проекция не сохраняет «вид» или «форму» мест. Вместо этого он растягивает, скручивает или сдавливает их. С другой стороны, сравните это с конформной коникой Ламберта (ниже), которая сохраняет общую форму массивов суши.
Эта проекция не сохраняет «вид» или «форму» мест. Вместо этого он растягивает, скручивает или сдавливает их. С другой стороны, сравните это с конформной коникой Ламберта (ниже), которая сохраняет общую форму массивов суши.
Подобные проекции называются конформными проекциями. Под капотом это свойство на самом деле немного сложнее: конформные проекции на самом деле сохраняют локальные углы. Но для картографов это сводится к тому, что места больше похожи на самих себя. В приведенном ниже примере Гренландия показана в трех конформных проекциях (верхний ряд) и трех неконформных проекциях (нижний ряд).
Обратите внимание, как конформные проекции делают Гренландию похожей на Гренландию. Форма немного меняется, и части острова становятся больше или меньше, но все они имеют одинаковую общую форму, даже если они не совсем похожи. Точно так же прямоугольник и квадрат имеют одинаковую общую «форму», несмотря на то, что они разные формы, тогда как квадрат и круг — нет.
Как и свойство равной площади, это свойство действует по принципу «все или ничего»; ваша проекция либо сохраняет формы везде на карте, либо нигде их не сохраняет.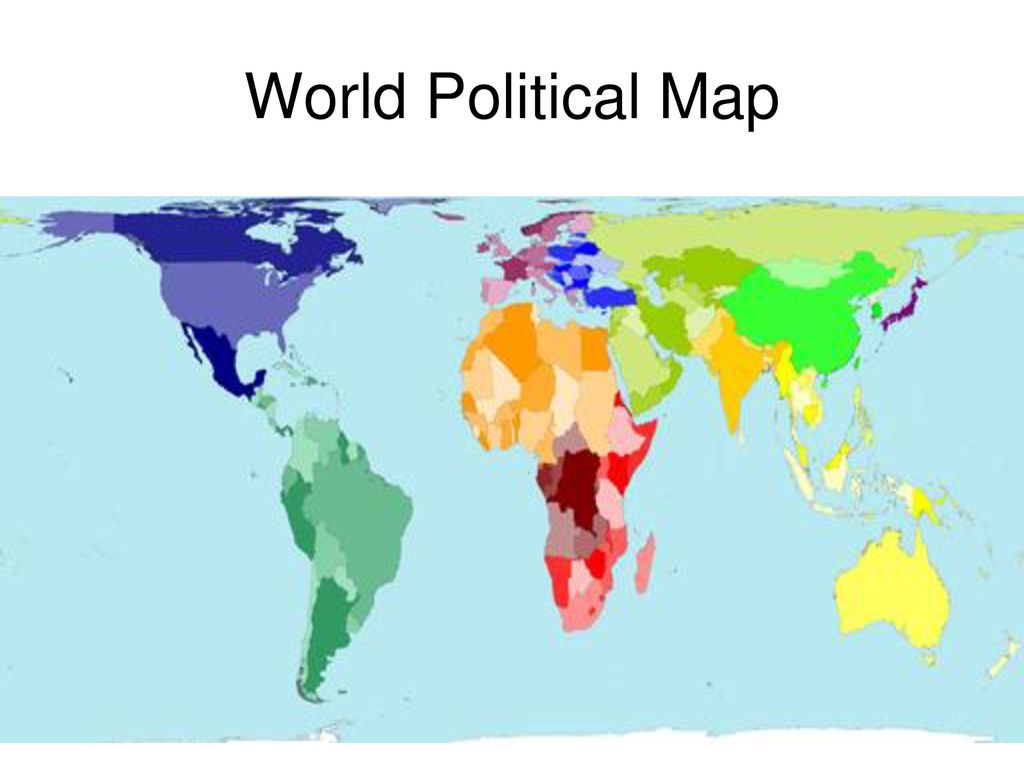
Расстояние — Большинство проекций искажают расстояния (например, равнопромежуточная проекция)
Поездка из Мэдисона в Буэнос-Айрес намного дальше, чем поездка из Мэдисона в Мадрид. Но в равнопрямоугольной проекции обе эти поездки выглядят одинаковой длины, потому что это проекция, которая не сохраняет расстояние. С другой стороны, азимутальная эквидистантная проекция показывает расстояния в правильной пропорции.
Но есть одна загвоздка. Хотя у нас есть картографические проекции, которые могут сохранять площади или формироваться повсюду на карте, нет такой, которая может сохранять расстояния повсюду. Существуют только проекции, которые позволяют сохранять расстояния относительно одной или двух точек на карте. Расстояния до и от центра карты азимутальной эквидистанты отображаются правильно, но расстояния между любыми другими двумя точками искажаются. Когда проекция сохраняет расстояние, мы называем ее равноудаленной .
Свойства площади, расстояния и формы исключают друг друга.Если у вас есть картографическая проекция, которая сохраняет одну, она исказит два других
Направления. Иногда прямая линия не является кратчайшим путем!
Нью-Йорк и Стамбул находятся почти на одной линии широты, около 41º северной широты. Это означает, что если вы направитесь на восток по прямой из Нью-Йорка, вы доберетесь до Стамбула. Но это не значит, что это кратчайшее расстояние между двумя городами.
На этом изображении есть линия, показывающая самый прямой и простой путь между Нью-Йорком и Стамбулом, который заключается в том, чтобы просто направить себя на восток и начать полет. Но изогнутая линия над ним показывает путь, по которому вам следует идти, если вы хотите пройти наименьшее расстояние, добираясь туда. Поскольку поверхность Земли искривлена, самые короткие пути вокруг нее тоже искривлены. Это может немного сбивать с толку, но имеет больше смысла, если вы попробуете это сделать сами: найдите глобус и прикрепите к нему кусок веревки. Приколите один конец к Нью-Йорку, а другой к Стамбулу и натяните нить. Вы заметите, что нить проходит точно по тому же пути, что и изогнутый маршрут на карте выше. Мы называем эти криволинейные пути кратчайшего расстояния большой круг маршрутов. С другой стороны, такой путь, как прямая линия, где вы все время держите себя в одном и том же направлении по компасу, называется прямой линией или локсодромией .
Вы заметите, что нить проходит точно по тому же пути, что и изогнутый маршрут на карте выше. Мы называем эти криволинейные пути кратчайшего расстояния большой круг маршрутов. С другой стороны, такой путь, как прямая линия, где вы все время держите себя в одном и том же направлении по компасу, называется прямой линией или локсодромией .
В некоторых проекциях, таких как проекция Меркатора выше, локсодромы показаны прямыми линиями. Они упрощают навигацию по воздуху и кораблям, потому что вам просто нужно провести прямую линию, направить свой корабль в этом направлении и начать плыть. В других проекциях маршруты большого круга показаны прямыми линиями, что позволяет легко определить кратчайшее расстояние между двумя точками. Стереографическая проекция — одна из них.
Теперь прямая линия — это большой круг, а изогнутая — локсодромия. Эти линии такие же, как и у Меркатора выше, но проекция меняет их внешний вид.
Когда проекция сохраняет маршруты большого круга в виде прямых линий, мы называем это азимутальной проекцией .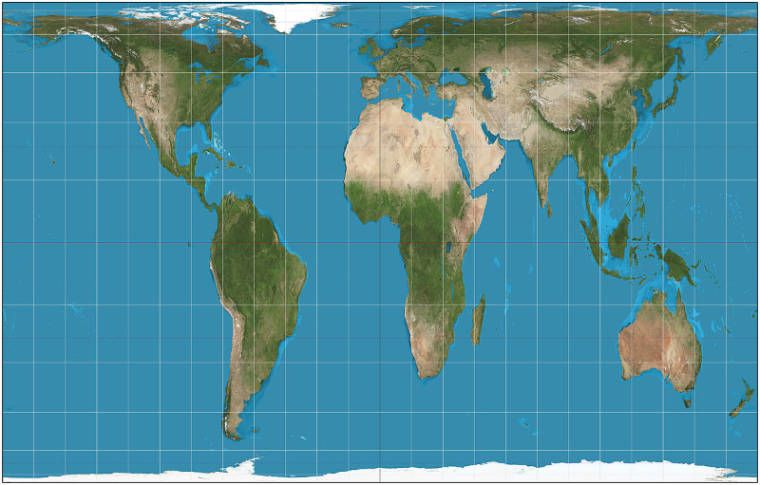 К сожалению, как и равноудаленные проекции, он работает только для одной точки за раз. На стереографическом изображении выше проекция сосредоточена на Нью-Йорке. Только прямые линии, входящие или исходящие из Нью-Йорка, будут большими кругами. Прямой линии между Мадридом и Касабланкой не будет.
К сожалению, как и равноудаленные проекции, он работает только для одной точки за раз. На стереографическом изображении выше проекция сосредоточена на Нью-Йорке. Только прямые линии, входящие или исходящие из Нью-Йорка, будут большими кругами. Прямой линии между Мадридом и Касабланкой не будет.
Компромиссы — ничего не делайте идеально, но большинство вещей достаточно хорошо
Если вы просмотрите приведенные выше примеры изображений, то заметите, что искажения, как правило, становятся все хуже и хуже по мере приближения к краям карты. . Обычно есть одна область, которая выглядит нормально и не слишком искажена, а затем все начинает сходить с ума, чем дальше вы отходите от этой области. Например, на азимутальной эквидистанте выше форма Австралии сильно искажена, но Британские острова выглядят нормально. Как правило, чем большую площадь показывает ваша карта, тем сильнее будут искажения, особенно по мере удаления от центра. Все это означает, что нас больше всего беспокоят искажения, когда мы делаем такие вещи, как картирование мира, и меньше, когда мы картируем небольшие области, такие как города или штаты.
Чтобы решить проблему карт мира с такими сильными искажениями по краям, люди придумали компромиссные проекции. Эти специальные проекции представляют собой компромиссы: в то время как большинство проекций имеют минимальные искажения в одной области, но сильно искажаются по мере удаления от этой области, компромиссные проекции искажают умеренную величину везде. Проекция Робинсона является одним из примеров компромиссной проекции:
Компромиссные проекции равномерно распределяют искажения. Плюс этого в том, что ни одно место не искажается до смешного. Именно поэтому компромиссные проекции хороши для карт мира. Недостатком является то, что больше нет особой области, которая почти не имеет искажений, как на большинстве других проекций. Вот почему компромиссные проекции не следует использовать для создания карт континентов, стран и всего, что не является всей Землей. Компромиссные проекции более равномерно распределяют искажения по всему миру, но если вы не показываете весь мир, вам не нужно ухудшать области карты с малыми искажениями, просто чтобы области с высокими искажениями (которые не край вашей карты) лучше.
Компромиссные проекции не сохраняют ни площади, ни формы, ни расстояния, но приближаются ко всем из них. В целом у них низкий уровень искажений, даже если они не сохраняют что-то конкретное. Если карта, которую вы создаете, требует сохранения чего-то конкретного, например площади, компромиссная проекция вам не подойдет.
Выбор проекции
Поскольку проекций очень много, возникает вопрос: какую из них выбрать? Как вы понимаете, тот факт, что их так много, означает, что не существует «лучшей» проекции. Каждый из них имеет свои преимущества и недостатки и лучше подходит для определенных ситуаций. Вот несколько вопросов, которые следует задать себе при выборе проекции:
Есть ли какое-то конкретное имущество, которое вам нужно сохранить? Помните, что некоторые проекции сохраняют площади, формы, расстояния или направления без искажений. Иногда объект вашего сопоставления лучше обслуживается сохранением одного из этих свойств. Вот несколько примеров:
- Площадь — Карты плотности требуют равновеликих проекций.
 Например, если вы работаете с набором данных о количестве людей на квадратную милю, ваша карта должна убедиться, что каждая квадратная миля выглядит одинакового размера. Если области искажаются, некоторые места начинают выглядеть более разреженными или более плотными, чем они есть на самом деле.
Например, если вы работаете с набором данных о количестве людей на квадратную милю, ваша карта должна убедиться, что каждая квадратная миля выглядит одинакового размера. Если области искажаются, некоторые места начинают выглядеть более разреженными или более плотными, чем они есть на самом деле. - Форма — Конформные проекции часто хороши для справочного картирования общего назначения, когда мы хотим, чтобы места выглядели узнаваемо и знакомо. Они также часто используются для навигационных карт. Сохраняя локальные углы, они не искажают траектории — поворот на 45º на Земле выглядит как поворот на 45º на карте, тогда как если бы углы были искажены, этого бы не было.
- Расстояние — Если вы хотите визуально показать, насколько далеко одна вещь от другой, вам нужно будет сохранять дистанцию. Иногда аэропорты используют их, чтобы показать города, в которые они летают.
- Направление — Также полезно для навигации.
 Иногда полезно изображать локсодромы прямыми линиями: Меркатор, например, был изобретен для моряков эпохи Возрождения, чтобы им было легче прокладывать курсы. Они могли провести прямую линию на карте, и это точно указывало бы им, по какому компасу идти домой. С другой стороны, если вы пилотируете самолет, вы можете изобразить большие круги прямыми линиями, чтобы добраться из пункта А в пункт Б с минимальным расходом топлива.
Иногда полезно изображать локсодромы прямыми линиями: Меркатор, например, был изобретен для моряков эпохи Возрождения, чтобы им было легче прокладывать курсы. Они могли провести прямую линию на карте, и это точно указывало бы им, по какому компасу идти домой. С другой стороны, если вы пилотируете самолет, вы можете изобразить большие круги прямыми линиями, чтобы добраться из пункта А в пункт Б с минимальным расходом топлива.
Есть много других причин сохранить каждое из этих свойств; приведенное выше — просто примеры, которые заставят вас задуматься. Некоторые другие соображения:
- Насколько велика область, которую вы наносите на карту? Если вы составляете карту мира (и вам не нужно сохранять конкретное свойство), лучше всего подойдет компромиссная проекция.
- Область вашей карты обычно проходит с севера на юг или с востока на запад? Различные проекции имеют разные модели искажений. Некоторые, такие как коническая равновеликая Альберса, искажают больше, когда вы идете на север или юг, но не искажают сильно, когда вы идете на восток или запад.
 Таким образом, они хороши для картографирования таких территорий, как Соединенные Штаты. Однако они не так хороши для картирования такой страны, как Чили, которая простирается с севера на юг. Поперечный Меркатор (в отличие от простого Меркатора) сильно искажает восток-запад, но не очень сильно искажает север-юг, поэтому он будет лучшим выбором для Чили.
Таким образом, они хороши для картографирования таких территорий, как Соединенные Штаты. Однако они не так хороши для картирования такой страны, как Чили, которая простирается с севера на юг. Поперечный Меркатор (в отличие от простого Меркатора) сильно искажает восток-запад, но не очень сильно искажает север-юг, поэтому он будет лучшим выбором для Чили. - Что подумают об этом ваши читатели? Например, хотя многие читатели могут быть знакомы с Меркатором, менее знакомые искажения, которые они видят на азимутальной эквидистанте, могут оттолкнуть их (или, возможно, заинтриговать их и заставить обратить больше внимания на вашу карту). Точно так же люди привыкли видеть, что США нанесены на карту чем-то вроде равновеликой коники Альберса, что придает им изогнутый вид; Созерцание США на цилиндрической равновеликой площади может показаться некоторым читателям неправильным, несмотря на то, что ни в одной из проекций нет ничего плохого.
Параметры проекции
Когда вы знаете, какую проекцию вы собираетесь использовать, остается последний шаг.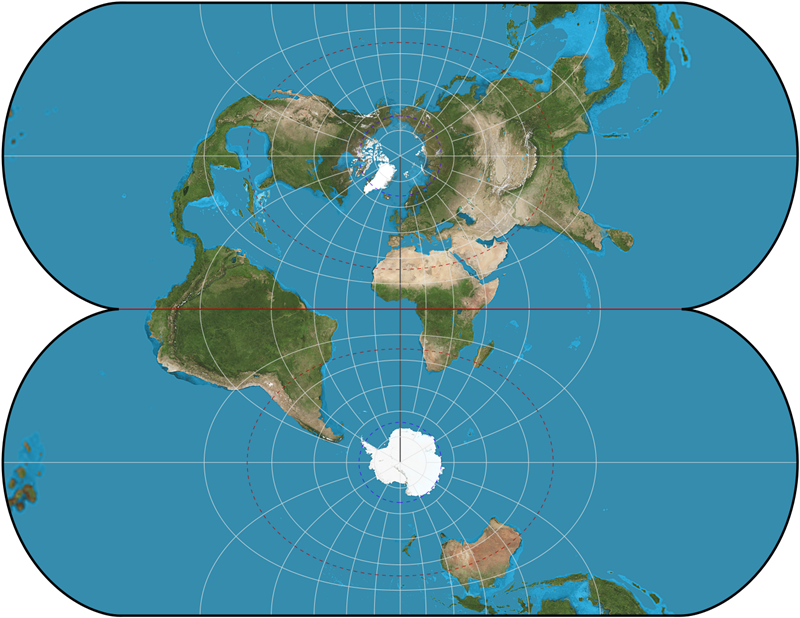 Как мы обсуждали выше, в каждой проекции есть места, где искажение хуже, и места, где оно не так уж плохо. К счастью, при настройке проекции мы можем выбрать место, где искажения минимальны. Это означает, что мы всегда можем убедиться, что объект нашей карты — это та часть, которая имеет наименьшее искажение. Мы делаем это, настраивая параметры проекции. Взгляните на эти две карты, сделанные в азимутальной равнопромежуточной проекции:
Как мы обсуждали выше, в каждой проекции есть места, где искажение хуже, и места, где оно не так уж плохо. К счастью, при настройке проекции мы можем выбрать место, где искажения минимальны. Это означает, что мы всегда можем убедиться, что объект нашей карты — это та часть, которая имеет наименьшее искажение. Мы делаем это, настраивая параметры проекции. Взгляните на эти две карты, сделанные в азимутальной равнопромежуточной проекции:
Оба используют одну и ту же проекцию, но имеют разные параметры. Карта слева настроена таким образом, чтобы центр области с наименьшим искажением находился вокруг Великих озер, а карта справа была сосредоточена на юго-востоке Австралии. Обе они по-прежнему являются азимутальными эквидистантными проекциями, что означает, что они правильно показывают расстояния при измерении от центра проекции, но каждая из них имеет разные центральные точки. Настраивая этот параметр, мы можем убедиться, что при использовании проекции она правильно настроена, чтобы показать область, которую мы хотим отобразить, с минимальными искажениями.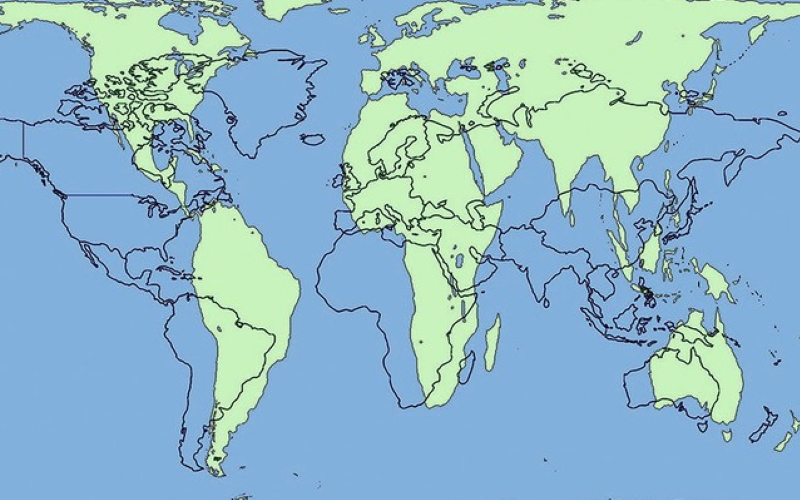
Различные проекции имеют разные параметры, которые вам нужно указать на основе их математической работы, которую мы пока оставим за кадром. Если для вашей проекции требуется центральная долгота и/или центральная широта, введите координаты, которые находятся в центре области, которую вы наносите на карту. Как и в приведенном выше примере, вы установите его так, чтобы проекция минимизировала искажения в области, которую вы отображаете.
Для некоторых проекций, таких как равновеликая коническая Альберса, необходимо ввести стандартных линий либо в дополнение к координатам центра, либо вместо них. Это линии широты, вдоль которых ваша проекция не будет иметь искажений. Например, стандартная линия на 30° с.ш. означает, что ваша проекция не будет иметь искажений на этой широте, хотя искажения будут распространяться на север и юг от этих линий – 31° с.ш. будет немного искажен, 32° с.ш. будет хуже, чем 31° с.ш. и т. д. Некоторые в проекциях нужна одна стандартная строка, в других можно ввести две. Если вы вводите его, установите стандартную линию на широту, которая находится в центре вашей карты; Опять же, мы следим за тем, чтобы область наименьшего искажения была областью, которую вы наносите на карту, а не где-то далеко. Если у вас есть возможность ввести две стандартные строки, лучше всего немного посложнее. Установите стандартные линии так, чтобы они делили вашу карту примерно на трети, как в примере ниже:
Если вы вводите его, установите стандартную линию на широту, которая находится в центре вашей карты; Опять же, мы следим за тем, чтобы область наименьшего искажения была областью, которую вы наносите на карту, а не где-то далеко. Если у вас есть возможность ввести две стандартные строки, лучше всего немного посложнее. Установите стандартные линии так, чтобы они делили вашу карту примерно на трети, как в примере ниже:
Делая это, вы убедитесь, что ни одна точка на вашей карте не находится очень далеко от стандартной линии — от одного из тех мест, где нет искажений. Это означает, что искажение сведено к минимуму по всей карте.
Наши рекомендации
При выборе картографической проекции никогда не бывает единственного «правильного ответа»; лучший выбор зависит от взвешивания всех факторов, описанных выше. Тем не менее, есть несколько фактов и практических правил, которые могут помочь сузить ваш выбор. Если вы работаете с веб-картами, у вас часто не будет выбора, кроме Меркатора.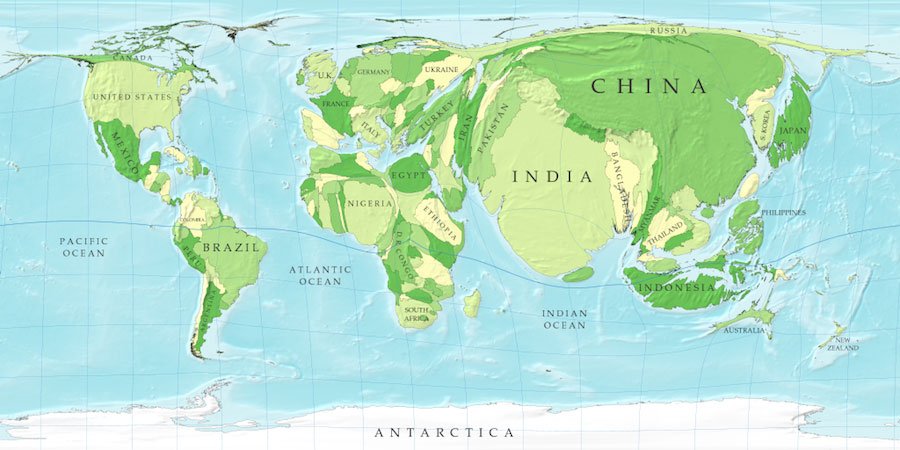

 Если у вас есть картографическая проекция, которая сохраняет одну, она исказит два других
Если у вас есть картографическая проекция, которая сохраняет одну, она исказит два других Например, если вы работаете с набором данных о количестве людей на квадратную милю, ваша карта должна убедиться, что каждая квадратная миля выглядит одинакового размера. Если области искажаются, некоторые места начинают выглядеть более разреженными или более плотными, чем они есть на самом деле.
Например, если вы работаете с набором данных о количестве людей на квадратную милю, ваша карта должна убедиться, что каждая квадратная миля выглядит одинакового размера. Если области искажаются, некоторые места начинают выглядеть более разреженными или более плотными, чем они есть на самом деле. Иногда полезно изображать локсодромы прямыми линиями: Меркатор, например, был изобретен для моряков эпохи Возрождения, чтобы им было легче прокладывать курсы. Они могли провести прямую линию на карте, и это точно указывало бы им, по какому компасу идти домой. С другой стороны, если вы пилотируете самолет, вы можете изобразить большие круги прямыми линиями, чтобы добраться из пункта А в пункт Б с минимальным расходом топлива.
Иногда полезно изображать локсодромы прямыми линиями: Меркатор, например, был изобретен для моряков эпохи Возрождения, чтобы им было легче прокладывать курсы. Они могли провести прямую линию на карте, и это точно указывало бы им, по какому компасу идти домой. С другой стороны, если вы пилотируете самолет, вы можете изобразить большие круги прямыми линиями, чтобы добраться из пункта А в пункт Б с минимальным расходом топлива. Таким образом, они хороши для картографирования таких территорий, как Соединенные Штаты. Однако они не так хороши для картирования такой страны, как Чили, которая простирается с севера на юг. Поперечный Меркатор (в отличие от простого Меркатора) сильно искажает восток-запад, но не очень сильно искажает север-юг, поэтому он будет лучшим выбором для Чили.
Таким образом, они хороши для картографирования таких территорий, как Соединенные Штаты. Однако они не так хороши для картирования такой страны, как Чили, которая простирается с севера на юг. Поперечный Меркатор (в отличие от простого Меркатора) сильно искажает восток-запад, но не очень сильно искажает север-юг, поэтому он будет лучшим выбором для Чили.